3.2 Постановка задачи 1
Постановка задачи 1
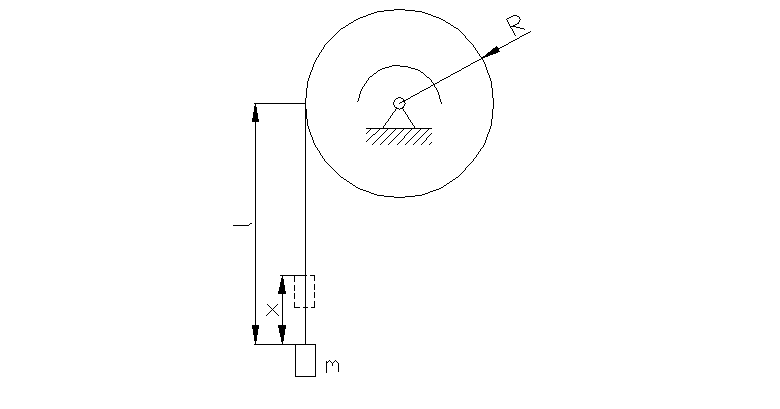
Груз массой ![]() укреплен на конце
упругого растяжимого безинарционного троса, намотанного на барабан. Составить
дифференциальное уравнение малых колебаний груза при равномерном вращении
барабана с угловой скоростью
укреплен на конце
упругого растяжимого безинарционного троса, намотанного на барабан. Составить
дифференциальное уравнение малых колебаний груза при равномерном вращении
барабана с угловой скоростью ![]() . Площадь поперечного
сечения троса
. Площадь поперечного
сечения троса ![]() , радиус барабана
, радиус барабана ![]() , модуль упругости материала троса
, модуль упругости материала троса ![]() .
.
Определить моменты времени, в которые груз проходит через
положение равновесия, считая, что в начальный момент времени ![]() длина размотанной части троса равна
длина размотанной части троса равна![]() , полная скорость движения
, полная скорость движения ![]() , а
, а ![]() (динамическое
удлинение троса). Получить решения частного случая:
(динамическое
удлинение троса). Получить решения частного случая: ![]() .
Принять
.
Принять ![]() кг,
кг, ![]() ГПа,
ГПа, ![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
 3.3 Постановка задачи 2
3.3 Постановка задачи 2
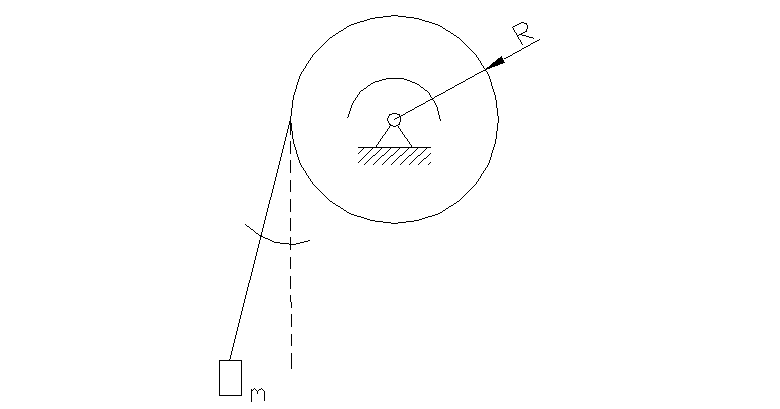
Груз массой ![]() укреплен на конце
абсолютно гибкого нерастяжимого безинарционного троса, намотанного на барабан. Составить
дифференциальное уравнение малых свободных поперечных колебаний груза при
равномерном вращении барабана с угловой скоростью
укреплен на конце
абсолютно гибкого нерастяжимого безинарционного троса, намотанного на барабан. Составить
дифференциальное уравнение малых свободных поперечных колебаний груза при
равномерном вращении барабана с угловой скоростью ![]() .
.
Получить зависимость амплитуды свободных колебаний от длины
свободного участка троса ![]() и угловой скорости
барабана
и угловой скорости
барабана ![]() . Рассмотреть опускание груза, приняв
следующие условия: при
. Рассмотреть опускание груза, приняв
следующие условия: при ![]() ,
, ![]() ,
, ![]() (
(![]() - угол отклонения троса
от вертикали).
- угол отклонения троса
от вертикали).
3.4 Исходные данные к проекту
 1.С использованием системы MathCAD рассчитать значения функций перемещения, скорости и ускорения динамической
системы с тросом. Построить графики этих функций (Задача 1).
1.С использованием системы MathCAD рассчитать значения функций перемещения, скорости и ускорения динамической
системы с тросом. Построить графики этих функций (Задача 1).
2.Определить момент времени, в который движущаяся масса проходит через положение равновесия.
3.Рассчитать значения функций перемещения, скорости и ускорения динамической системы с тросом. Построить графики новых функций (Задача 2).
4.Исследовать влияние угловой скорости барабана и длины свободного участка троса на амплитуду свободных колебаний системы.
5.Вычислить аналитические аппроксимирующие функции по результатам исследований предыдущего пункта. Построить графически исходные и аппроксимирующие зависимости.
3.5 Описание реализации задач и выводы
Задача 1. В процессе вертикальных колебаний на груз
действуют сила инерции ![]() , сила тяжести
, сила тяжести ![]() и восстанавливающая сила
и восстанавливающая сила![]() . Дифференциальное уравнение имеет вид:
. Дифференциальное уравнение имеет вид:
![]() (1)
(1)
где ![]() . Полное напряжение
. Полное напряжение ![]() в тросе можно рассматривать как сумму
статического напряжения и напряжения, вызванного удлинением троса
в тросе можно рассматривать как сумму
статического напряжения и напряжения, вызванного удлинением троса ![]() при колебаниях груза:
при колебаниях груза:
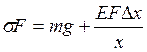 (2)
(2)
где ![]() . С учетом (2)
представим уравнение (1) в виде:
. С учетом (2)
представим уравнение (1) в виде:
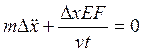 (3)
(3)
Выразим из уравнения (3) ![]() :
:
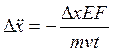 (4)
(4)
Для решения этого дифференциального уравнения в системе MathCAD разобьем его на систему дифференциальных уравнений первого порядка:
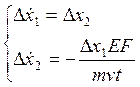
Решив эту систему, строим графики перемещения, скорости. График ускорения получаем, вычислив уравнение (4) (см. приложение 1). Графики скорости и ускорения затухающие, а на графике перемещения постепенно устанавливаются свободные колебания.
 Для
нахождения момента времени, когда груз проходит через положение равновесия, используем
следующую формулу:
Для
нахождения момента времени, когда груз проходит через положение равновесия, используем
следующую формулу:
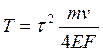
Аналитический результат составил ![]() , результат из графика
, результат из графика ![]() . Погрешность составляет
. Погрешность составляет ![]() (см. приложение 1).
(см. приложение 1).
Задача 2.Применим
уравнение Лагранжа второго рода. Положение тела в любой момент времени
определяется двумя координатами: углом отклонения от положения статического
равновесия ![]() и длиной размотанной части троса
и длиной размотанной части троса ![]() . Поскольку
. Поскольку ![]() -
известная функция времени, в качестве обобщенной координаты выберем угол
-
известная функция времени, в качестве обобщенной координаты выберем угол ![]() . Кинетическая энергия движущегося груза:
. Кинетическая энергия движущегося груза:
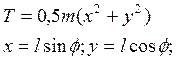
следовательно ![]() .(1)
.(1)
Потенциальная энергия груза в отклоненном положении
![]() (2).
(2).
Подставим (1) и (2) в уравнение Лагранжа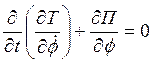 получим дифференциальное уравнение в виде:
получим дифференциальное уравнение в виде:
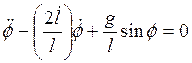 .
.
![]() ,
, ![]() получаем:
получаем:
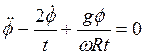 .
.
![]() ,так как
рассматриваем опускание груза, то
,так как
рассматриваем опускание груза, то
![]() ,
, ![]()
и, следовательно, дифференциальное уравнение примет вид:
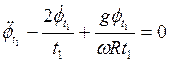 .
.
Для решения этого дифференциального уравнения в системе MathCAD, как и в предыдущей задаче разобьем его на систему дифференциальных уравнений первого порядка:
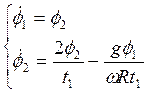
Аналогично строим все графики (см. приложение 2).
В приложениях 3 и 4 представлены опыты
по изменению длины свободного участка троса l и угловой скорости барабана ![]() соответственно,
и проведена аппроксимация данных.
соответственно,
и проведена аппроксимация данных.
 Из
опытов видно, что изменение длины свободного участка троса существенного
влияния не оказывает. Чем больше l, тем
медленнее растет амплитуда колебаний. Изменение угловой скорости барабана
оказывает большее влияние. При увеличении f колебания усиливаются очень быстро, быстро растет
амплитуда.
Из
опытов видно, что изменение длины свободного участка троса существенного
влияния не оказывает. Чем больше l, тем
медленнее растет амплитуда колебаний. Изменение угловой скорости барабана
оказывает большее влияние. При увеличении f колебания усиливаются очень быстро, быстро растет
амплитуда.
При проведении опытов параметры ![]() и
и ![]() принимали
следующие значения:
принимали
следующие значения:
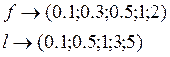
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.