Определение скоростей и ускорений точек твердого тела при поступательном движении. Определение абсолютной скорости и абсолютного ускорения точки в случае вращательного переносного движения

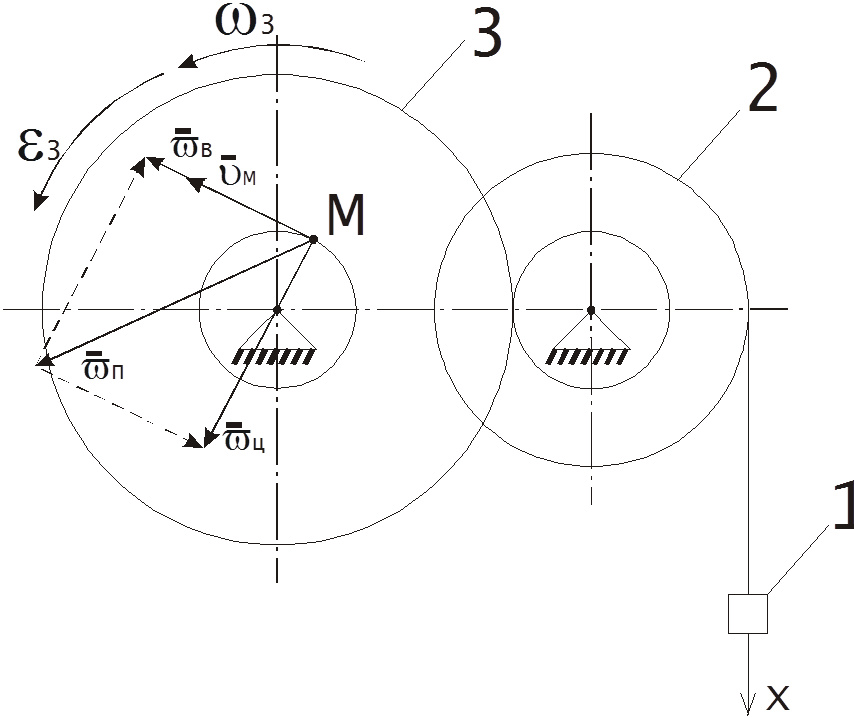
Поступательное и вращательное движение твердого тела.

 см.        см.                          

 м.        см.                    см.                    

Решение:

1.  Найдем момент времени , когда путь ,  пройденный грузом =  м.

. Выразим :  c.

2.  Найдем скорость груза:  см/с.

3.  Угловая скорость звена 2 равна :  Гц.

4.  Т.к. колеса 2 и 3 связаны зубчатым зацеплением, то их угловые скорости

обратно пропорциональны их радиусам  =>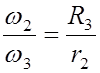

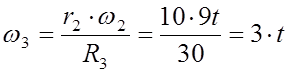 Гц.

5.  Найдем угловое ускорение :  c^-2.

6.  Линейная скорость точки М:  см/с. Скорость  направлена перпендикулярно к радиусу в сторону вращения колеса 3.

7.  Вращательное ускорение точки М: см/с². Вращательное ускорение  сонаправлено со скоростью  т.к. вращение колес ускоренное.

8.  Центростремительное ускорение точки М:  см/с². Ускорение  направлено к центру колеса.

9.  Полное ускорение точки М: в векторном виде - . Модуль полного ускорения - 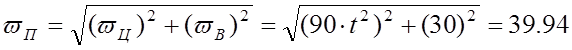 см/с².

10.  Подставляем в найденные формулы  вместо  получим:  см/с, см/с²,  см/с²,  см/с².

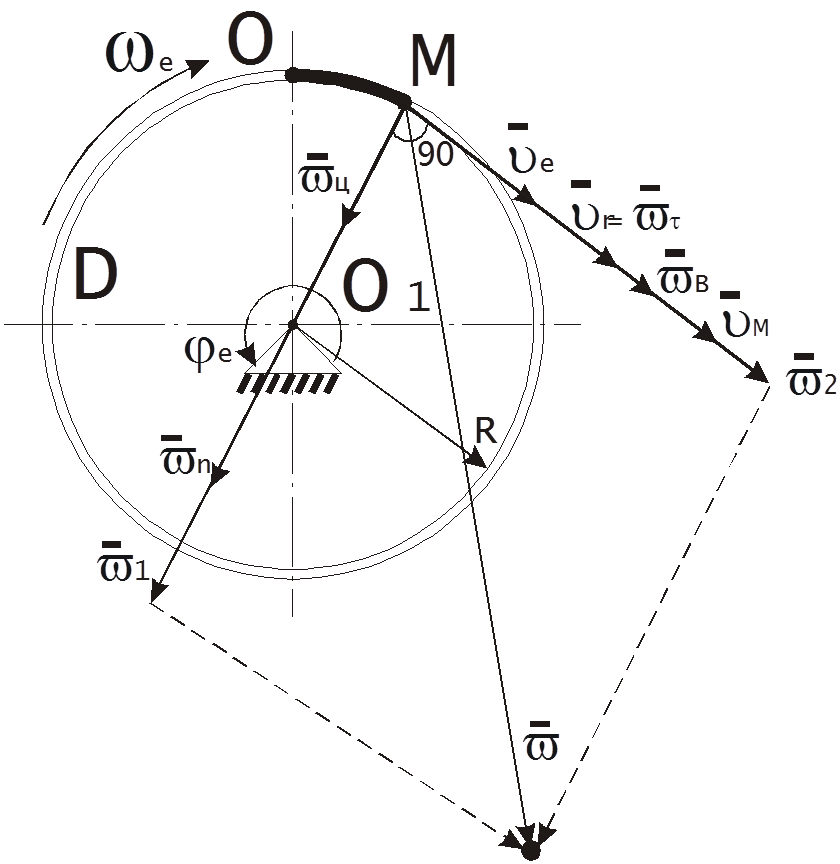
Сложное движение точки.

 рад.                             см.          

 м.              с.     

Решение:

1.  Найдем абсолютную скорость : .

2.  Модуль относительной скорости:  см/с. В момент времени ,  см/с. Знак плюс перед модулем относительной скорости показывает, что она направлена в сторону увеличения ОМ.

3.  Модуль переносной скорости:  см/с. В момент времени ,  см/с. Знак плюс перед модулем переносной скорости показывает, что она направлена в сторону увеличения угла .

4.  Так как вектора относительной и переносной скоростей направлены одинаково, по касательной к окружности D, то вектор абсолютной скорости  сонаправлен с ними, а его модуль есть сумма модулей  и :  см/с.

5.  Найдем абсолютное ускорение : .

6.  Нормальное ускорение : направлено к центру окружности D, а его модуль равен  см/с².

7.  Касательное ускорение : направлено по касательной к окружности D, а его модуль равен  см/с².

8.  Вращательное ускорение : направлено по касательной к окружности D, а его модуль равен см/с². Знак плюс перед модулем вращательного ускорения показывает, что оно направлено в сторону увеличения угла .

9.  Центростремительное ускорение : направлено к центру окружности D, а его модуль равен  см/с².

10.  Кориолисово ускорение: , по модулю , но так как векторы  и  сонаправлены, то . Следовательно, кориолисово ускорение равно 0.

Абсолютное ускорение : в векторном виде - . Направление абсолютного ускорения показано на рисунке. Модуль абсолютного ускорения найдем по правилу паралеллограма -

11.   см/с².

12.  Результаты вычислений:  см/с,  см/с².

Список литературы:

1.  Яблонский А.А., Норейко С.С. Сборник заданий для курсовых работ по теоретической механике. –М.:Высш.шк.,1972.

2.  Федута А.А., Чигарев А.В. Теоретическая механика и методы математики.    –М.:”Технопринт”, 2000.

3.  Акимов В.А., Скляр О.Н. Сборник задач по теоретической механике с решениями. Часть II. –М.:”Технопринт”, 2001.

4.  Мещерский И.В. Сборник задач по теоретической механике. –М.: Наука, 1986.