Анализ переходных процессов при исследовании динамических моделей технических систем. Навыки выполнения анализа переходных процессов в динамических моделях с графической интерпретацией полученных результатов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО

Факультет автоматизированных и информационных систем

Кафедра «Информатика»

ОТЧЕТ   ПО   ЛАБОРАТОРНОЙ   РАБОТЕ   № 5

по дисциплине «Компьютерные методы инженерного моделирования»

на тему: Анализ переходных процессов при исследовании динамических моделей технических систем.

Выполнил:      студент гр. ИТ-32

Принял:           преподаватель

      

Дата сдачи отчета:         _____________________

Дата допуска к защите: _____________________

Дата защиты:                 _____________________

Гомель 2012

Лабораторная работа №5.

Анализ переходных процессов при исследовании динамических моделей технических систем.

Цель работы: Получить навыки выполнения анализа переходных процессов в динамических моделях с графической интерпретацией полученных результатов.

Порядок выполнения работы

Все пункты порядка выполнения работы применить к индивидуальным техническим объектам, математические модели и описание которых приведены в папке «Задачи».

1 часть

1.  Получить функции возмущающей силы:

А) F(t) = F0sin(wt) – гармоническое воздействие;

Б) H(t) - функция Хевисайда – ступенчатое воздействие.

2.  Рассчитать значение функции перемещения динамической системы без воздействия начальных значений перемещения и скорости с учетом гармонической возмущающей силы F(t). Построить график этой функций.

3.  Рассчитать значение функции перемещения динамической системы без воздействия начальных значений перемещения и скорости с учетом ступенчатого воздействия. Построить график этой функций.

4.  Для функции перемещения п.3 рассчитать следующие параметры переходного процесса:

- коридор стабилизации установившегося состояния;

- время переходного процесса;

- коэффициент динамичности;

- декремент колебаний;

- колебательность.

Выполнить графическую интерпретацию первых двух результатов.

Задача 5

Исходными данными для работы являются:

m– масса груза

2l–длина стержня

D – диаметр пружины

d– диаметр проволоки пружины

G – модуль упругости материала пружины

i – число витков пружины

α – коэффициент вязкого сопротивления.

Таблица 5.1 - Таблица исходных данных

l (м)	D(мм)	d (мм)	i	m (кг)	α	φ0	tк  (с)	Варьируемый параметр	N варианта
0,28	22	1,8	5	18	72	0.08	1	m	5

G=80·10⁹Па

Описание математической модели

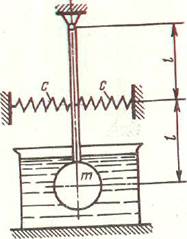
Дан абсолютно жесткий стержень, на котором подвешен груз массой m. Длина стержня равна 2l. К середине стержня прикреплены две упругие растяжки-пружины жесткостью с каждая. Груз помещен в сосуд, заполненный вязкой жидкостью.

В процессе малых свободных колебаний груза жидкость оказывает  демфирующее влияние на систему.

Дифференциальное уравнение свободных колебаний груза запишем в ви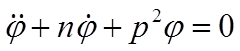де:

,где

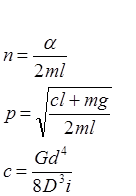
Здесь n – коэффициент вязкого сопротивления;

p – частота собственных колебаний системы;

с – жесткость пружины.

F(t) = F₀sin(wt) – возмущающая сила, действующая на систему. Все параметры функции подобрать самостоятельно.

Листинг программы  в Matlab:

KMIM_Laba_05_01.m

disp('___________Вариант_5_5_____________')

clear all;            %..Очистка_перменных

close all;          %..закрытие_окон

l=0.28;             %..Длина_стержня

D=22*10^-3;         %..Диаметр_стержня

d=1.8*10^-3;        %..Диаметр_проволки_пружины

i=5;                %..Число_витков

m=18;               %..Масса_груза

a=72;               %..Коэффициент_вязкости

fi0=0.08;           %..Начальный_угол

t_k=10;             %..Время

G=80*10^9;          %..Модуль_упругости_материала_пружины

disp(' __________________________________Исходные_данные________________________________________ ');          %..вывод_в_командное_окно

disp('|    l    |    D    |    d    |    i    |    a    |   fi0   |   t_k   |    G    |    m    |');          %..вывод_в_командное_окно

fprintf('| %7.5g | %7.5g | %7.5g | %7.5g | %7.5g | %7.5g | %7.5g | %7.5g | %7.5g |\n',l,D,d,i,a,fi0,t_k,G,m); %..вывод_в_командное_окно_значений_исходные_данных

disp('|_________|_________|_________|_________|_________|_________|_________|_________|_________|');          %..вывод_в_командное_окно

%..Получить_функции_возмущающей_силы:_гармоническое_воздействие,функция_Хевисайда_ступенчатое_воздействие.

t=0:0.001:1;    %..время_процесса

F0=3;           %..возмущающая_сила

w=15;           %..частота