for i=1:length(T) %..цикл
if (T(i)<=0.5) %..оператор_выбора
H(i)=0;
else H(i)=1;
end;
end;
subplot(3,1,3);
plot(T,H,'g'); %..график_ступенчатого_воздействия
xlabel('t'); %..служит_для_вывода_название_координаты_X
ylabel('H'); %..служит_для_вывода_название_координаты_Y
title('График возмущающей силы с учетом ступенчатого воздействия') %..служит_для_вывода_название_графика
grid; %..сетка
%..4.Для функции перемещения п.3 рассчитать следующие параметры переходного процесса:- коридор стабилизации установившегося состояния; - время переходного процесса;- коэффициент динамичности;- декремент колебаний; - колебательность.Выполнить графическую интерпретацию первых двух результатов.
%..коридор_стабилизации_установившегося_состояния
Del_s=Y(length(Y(:,1)),1);
Del_v=Del_s+Del_s*0.05;
Del_n=Del_s-Del_s*0.05;
%..время_переходного_процесса
index=length(Y(:,1));
while (index>1)%..цикл
if (Y(index-1,1)>=Del_v)||(Y(index-1,1)<=Del_n)%..оператор_выбора
T_n=T(index);
index_t=index;
index=0;
end;
index=index-1;
end;
T_n=T_n-0.5;
%..Графическая_интерпретация_времени_переходного_процесса_и_коридора_стабилизации_установившегося_состояния
figure(4); %..создаем_графическое_окно
clf() %..очистка_графического_окна
plot(T,Y(:,1),[T(1),T(length(T))],[Del_s,Del_s],'r--',[T(1),T(length(T))],[Del_v,Del_v],'r--',[T(1),T(length(T))],[Del_n,Del_n],'r--',[T_n+0.5,T_n+0.5],[Del_s,max(Y(:,1))],'-.g',[0.5,0.5],[Del_s,max(Y(:,1))],'-.g',[T_n+0.5,0.5],[max(Y(:,1)),max(Y(:,1))],'-g'); %..график_перемещения_с_учетом_ступенчатого_воздействия
xlabel('T'); %..служит_для_вывода_название_координаты_X
ylabel('H'); %..служит_для_вывода_название_координаты_Y
text( T_n,max(Y(:,1))+0.0003 , 'Tn' ); %..служит_для_вывода_текста_на_графике
text( T(length(T)),Del_s+0.00015, '\leftarrowDelta' ); %..служит_для_вывода_текста_на_графике
title('График S(t) с учетом ступенчатого воздействия') %..служит_для_вывода_название_графика
grid; %..сетка
[Amax,n_max] = max(Y(:,1)); %..максимальная_Амплитуда
Kd=1+Amax/Del_s; %..коэффициент_динамичности
%..Дикремент_колебаний
index=n_max+1;
while (index<length(Y(:,1)))
if(Y(index,1)>Y(index-1,1))&&(Y(index,1)>Y(index+1,1))
A2=Y(index,1);
index=length(Y(:,1));
end;
index=index+1;
end
Dek=Amax/A2;
%..Колебательность
count=0;
k=0;
for index=2:index_t-1
if(Y(index,1)<=Del_s)&&(Y(index+1,1)>Del_s)
count=count+1;
end;
end;
disp(' __________________________________Результат_вычислений_________________________ '); %..вывод_в_командное_окно
disp('| Tn | Dek | Kd | count | Del_s | Del_n | Del_v | Amax |'); %..вывод_в_командное_окно
fprintf('| %7.5g | %7.5g | %7.5g | %7.5g | %7.4g | %7.4g | %7.4g | %7.4g |\n',T_n,Dek,Kd,count,Del_s,Del_n,Del_v,Amax); %..вывод_в_командное_окно_значений_исходные_данных
disp('|_________|_________|_________|_________|_________|_________|_________|_________|'); %..вывод_в_командное_окно
vid1.m
function ur2 = vid1(t,y,n,p,F0,w)
ur2=zeros(2,1);
ur2(1)=y(2); %..перемещение с учетом гармонической возмущающей силы F(t)
ur2(2)=-n*y(2)-p^2*y(1)+F0*sin(w*t); %..скорость с учетом гармонической возмущающей силы F(t)
end
vid2.m
function ur2 = vid2(t,y,n,p)
ur2=zeros(2,1);
if (t<0.5)
H=0;
else H=1;
end
ur2(1)=y(2); %..перемещение с учетом гармонической возмущающей силы F(t)
ur2(2)=-n*y(2)-p^2*y(1)+H; %..скорость с учетом гармонической возмущающей силы F(t)
end


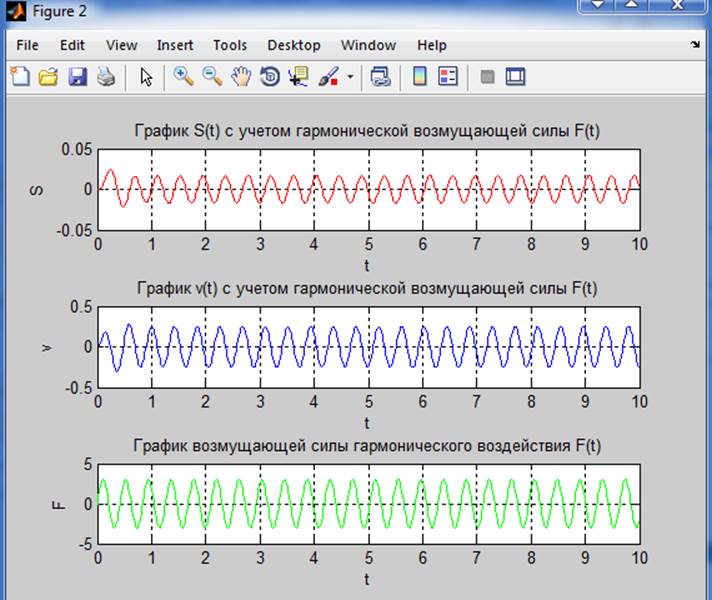
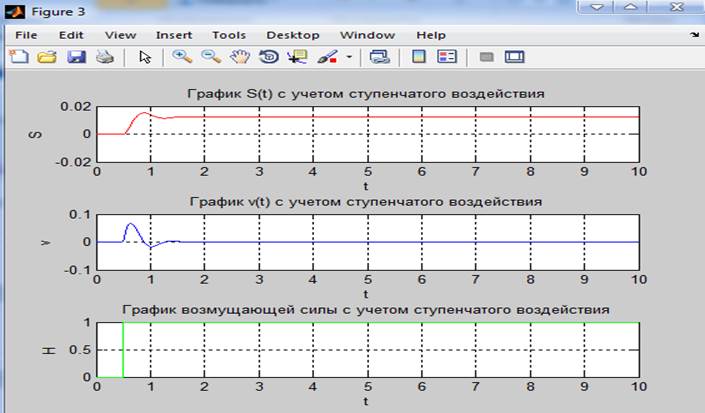
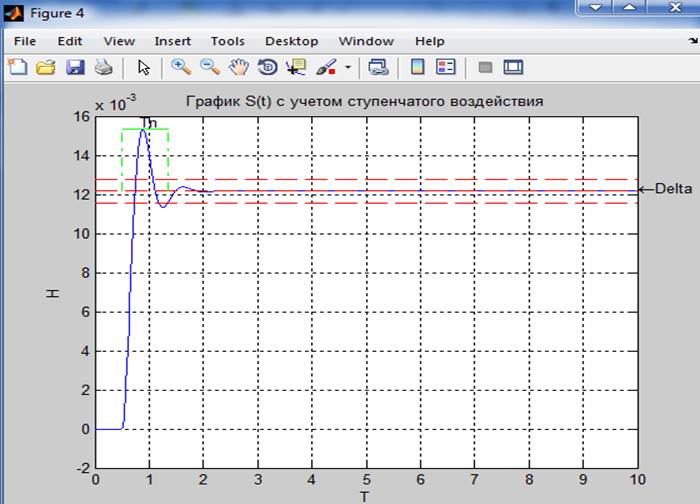
Вывод:Получили навыки выполнения анализа переходных процессов в динамических моделях с графической интерпретацией полученных результатов. В результате моделирования мы получили функции гармонического и ступенчатого взаимодействия. Рассчитали значение функции перемещения динамической системы без воздействия начальных значений перемещения и скорости с учетом гармонической возмущающей силы F(t). Построили график этих функций. Тоже самое проделали с учетом ступенчатого воздействия. Для функции перемещения с ступенчатым взаимодействием рассчитали такие параметры как коридор стабилизации установившегося состояния, время переходного процесса 0.85, коэффициент динамичности 2.26, декремент колебаний 1.23, колебательность 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.