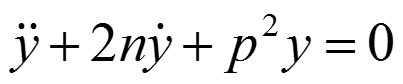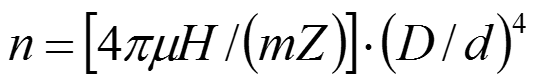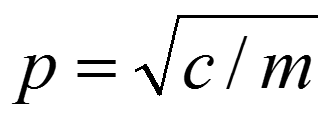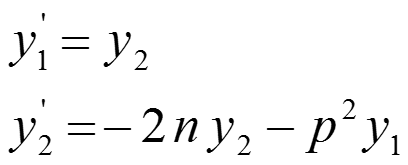Пример 1
-
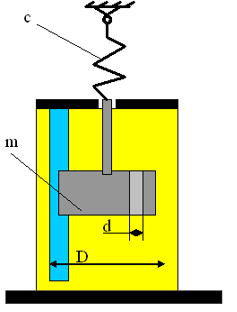
Дан гидравлический демпфер, представляющий собой поршень массой m, движущийся в жидкости. Уравнение движения демпфера имеет вид:
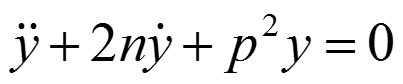
-
где n - приведенный коэффициент вязкого сопротивления вычисляется по формуле:
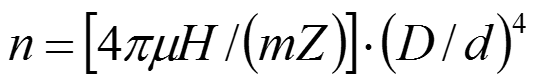
-
p – частота собственных колебаний системы вычисляется по формуле:
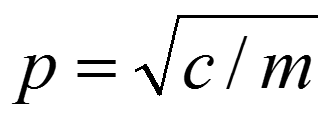
-
Алгоритмический анализ задачи
-
Исходными данными для решения задачи являются:
-
y0 –отклонение поршня демпфера от положения равновесия;
-
m – масса поршня;
-
с – жесткость пружины;
-
μ – динамический коэффициент вязкости жидкости;
-
D – диаметр цилиндра;
-
d – диаметр отверстия;
-
H – высота поршня;
-
z –число отверстий.
-
Для решения дифференциального уравнения в Matlab его нужно привести к системе из двух дифференциальных уравнений вида:
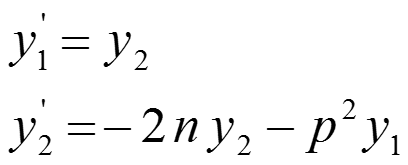
-
При реализации модели в системе Matlab нужно создать два М-файла, один из которых будет являться функцией, описывающей вид решаемой системы дифференциальных уравнений, а другой – программой, выполняющей расчет с обращением к этой функции и к стандартной функции для решения дифференциальных уравнений ode45.
-
Пусть М-файл функции, описывающей вид решаемой системы дифференциальных уравнений, называется vid2.m, а М-файл вызывающей программы – GD.m, тогда порядок выполнения расчетов в системе Matlab будет следующим.
-
Создать М-файл вызывающей программы – GD.m, в котором:
-
- создать вектор y0 начальных условий;
-
- получить вектор T и матрицу Y как результаты работы функции для решения дифференциальных уравнений ode45, причем Т содержит дискретные значения времени расчета модели, первый столбец матрицы Y – значения перемещения, второй столбец – значения скорости.
-
- построить графики функций перемещения и скорости по соответствующим столбцам матрицы Y в зависимости от вектора T.
-
Создать М-файл функции, описывающей вид решаемой системы дифференциальных уравнений, называется vid2.m, в котором:
-
- задать исходные данные для решения задачи;
-
- вычислить значения n и p;
-
- создать вектор ur2 из двух элементов, в котором описать систему дифференциальных уранений.
-
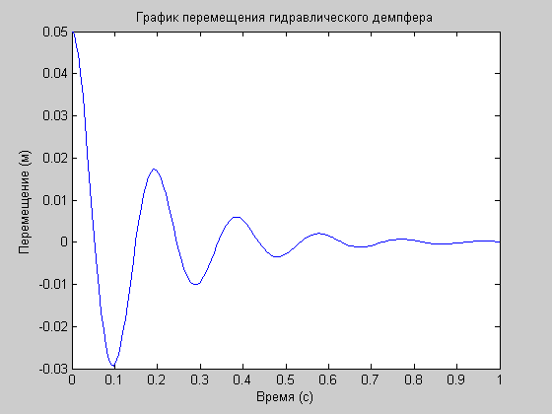
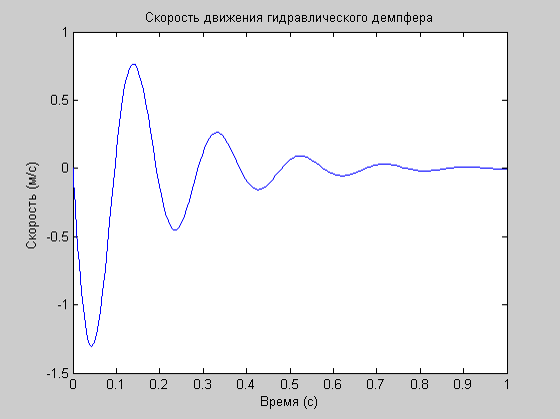
Запустить М-файл GD1 на выполнение, получить результаты расчетов по модели и графическую интерпретацию результатов в окнах отображения графической информации Figure 1 и Figure 2.
Основная программа
% Задание начальных условий
y0=[0.05 0];
% Решение дифференциального уравнения
[T,Y]=ode45(@vid2,[0 1],y0);
% Графики функций перемещения и скорости демпфера
figure(1)
plot(T,Y(:,1))
figure (2)
plot(T,Y(:,2))
Функция
function ur2=vid2(t,y);
ur2=zeros(2,1);
% Исходные данные
m=2.73; H=0.05; c=3e3; D1=0.1; d=0.01; z=25; mu=6e-2;
% Расчет приведенного коэффициента вязкого сопротивления
Функция
% и частоты собственных колебаний демпфера
p=sqrt(c/m); n=4*pi*mu*H/(m*z)*(D1/d)^4;
% Описание системы дифференциальных уранений
ur2(1)=y(2);
ur2(2)=-2*n*y(2)-p^2*y(1);
-
Создадим модель с проведением серии экспериментов по модели.
-
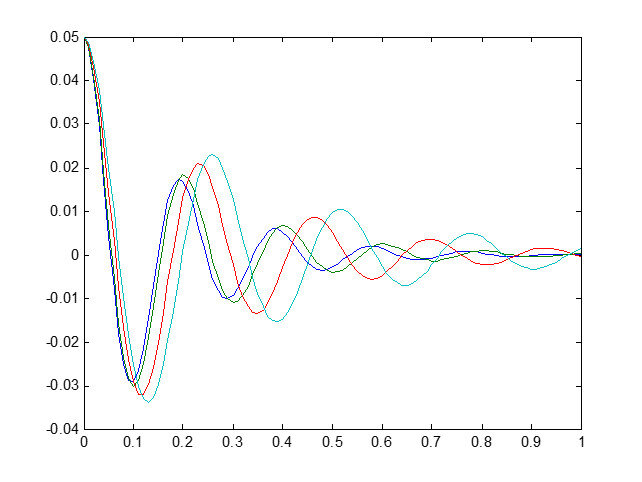
Выберем в качестве варьируемого параметра m –масса поршня.
% Задание начальных условий
y0=[0.05 0]; M=[2.73,3,4,5];
for i=1:length(M),
m=M(i);
% Решение дифференциального уравнения
diap=0:0.01:1
[T,Y]=ode45(@vid2,diap,y0,[],m);
R(:,i)=Y(:,1);
end
% Графики функций перемещения и скорости демпфера
figure(1)
plot(T,R(:,1:length(M)))
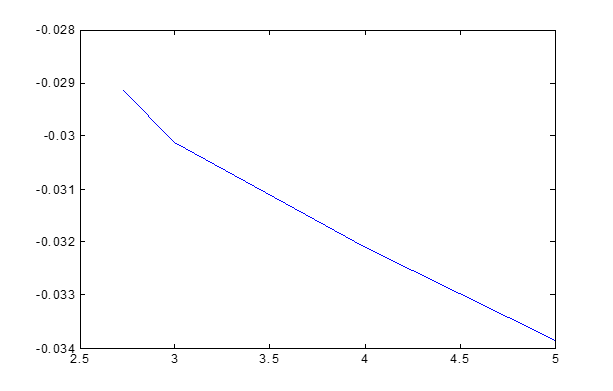
MR=min(R);
figure(2)
plot(M,MR)
Символьная модель
syms y p n R t de
de = 'D2y + 2*n*D1y + p^2*y' ;
R = dsolve (de, 'y(0)=0.05, Dy(0) = 0')
pretty(R)
H=0.05; c=3e3; D11=0.1; d=0.01; z=25; mu=6e-2; m=2.73;
t=str2num('t');
n=str2num('n');
p=str2num('p');
p=sqrt(c/m); n=4*pi*mu*H/(m*z)*(D11/d)^4;
X=0:0.01:1;
for i=1:length(X(1,:)),
t=X(i);
Ut1(i)=subs(R);
end
plot(X,Ut1)
Пример 2
Электрическая цепь описывается передаточной функцией вида:
K = 1/(p*tau + 1)
tau – заданный коэффициент.
Входной сигнал имеет вид:
S(t)=A*exp(-α*t)
syms A alpha t st Stt a s p K tau Ut
st = knf(t,A,alpha)
Stt = laplace(st,t,p)
K = 1/(p*tau + 1)
U = Stt*K
Ut=ilaplace(U,p,t)
Ut=simplify(Ut)
A=str2num('A');
A=1;
tau=str2num('tau');
tau=0.5;
alpha=str2num('alpha');
alpha=0.3;
t=str2num('t');
X=0:0.01:5;
for i=1:length(X(1,:)),
t=X(i);
Ut1(i)=subs(Ut);
st1(i)=subs(st);
end
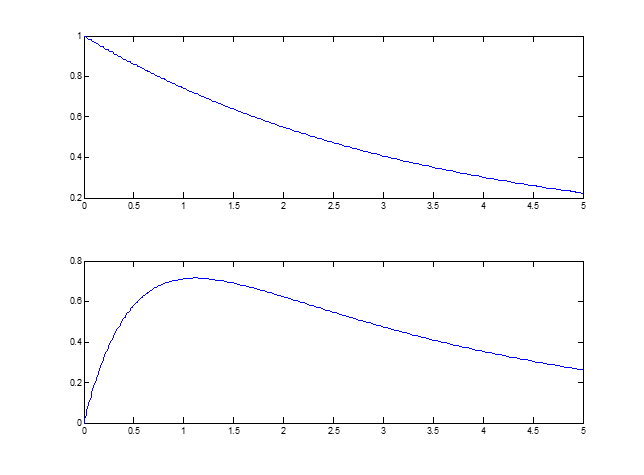
subplot(2,1,2)
plot(X,Ut1)
subplot(2,1,1)
plot(X,st1)
function sstt=knf(t,AF,BF);
sstt=AF*exp( - BF * t );