Математика \ Высшая математика

Конические сечения. Возможные сечения плоскостью, проходящей через вершину конической поверхности

Страницы работы

25 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Конические сечения

Начать показ

Оглавление

Конические сечения Эллипс Парабола Гипербола Контрольная работа

Дальше

Конические сечения

Коническая поверхность — фигура, полученная вращением прямой (образу-ющей) вокруг другой прямой, пересека-ющей её под острым углом, называемой осью вращения.

Дальше

Возможные сечения плоскостью, проходящей через вершину конической поверхности

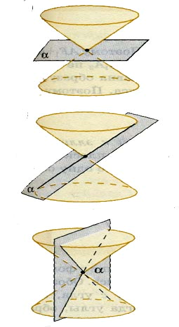
Если плоскость проходит через вершину конической поверхности, то в сечении может получиться: 1) точка; 2) прямая (образующая); 3) две пересекающиеся прямые (образующие).

Дальше

Эллипс

Эллипсом (рис. 1) называ-ется геометрическое место точек, сумма расстояний от которых до двух заданных точек F1 и F2, называемых фокусами эллипса, есть величина постоянная.

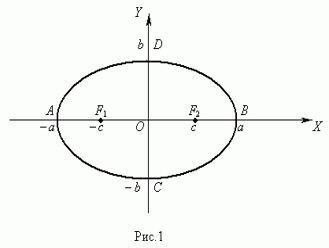
Рис. 1

Дальше

Эллипс. Фокальное свойство

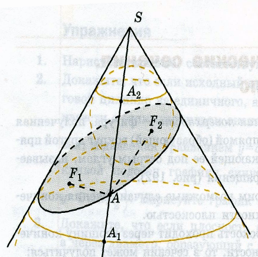
Пусть плоскость не проходит через вершину S конической поверхности. Обозначим через φ угол между образующей и осью вращения. Докажем, что если плоскость сечения пересекает ось под углом, большим φ, то в сечении получается эллипс. Для этого достаточно доказать, что сечение удовлетворяет следующему фокаль-ному свойству: Сумма расстояний от произвольной точки сечения до двух данных точек есть величина постоянная.

Дальше

Доказательство фокального свойства

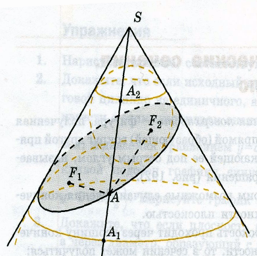
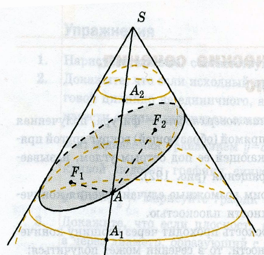
Доказательство. Впишем в коническую поверхность две сферы, касающиеся плоскости сечения в некоторых точках F1, F2 и конической поверхности по окружностям C1 и C2. Пусть А — произвольная точка сечения. Проведем образующую АS и обозначим через A1, A2 точки ее пересечения с окружностями C1 и C2. Заметим, что прямая АS является касательной к обеим сферам.

Дальше

Доказательство фокального свойства

Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF1 = AA1, AF2 = AA2. Поэтому AF1 + AF2 = AA1 + AA2 = A1A2. Но длина отрезка A1A2 не зависит от выбора точки А сечения. Она равна образующей соответствующего усечен-ного конуса. Поэтому сумма расстояний от точки А до точек F1 и F2 будет постоянной.

Дальше

Касательная к эллипсу. Свойство касательной

Определение. Касательной к эллипсу называется прямая, лежащая в плоскости эллипса и имеющая с ним только одну общую точку.
Теорема. Углы между каса-тельной к эллипсу и отрезками, соединяющими точку касания с фокусами эллипса равны.

Дальше

Свойство касательной

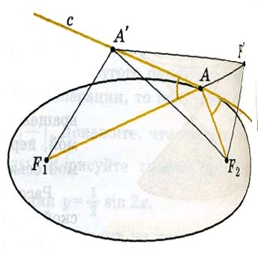
Доказательство. Пусть задан эллипс с фокусами F1, F2 и А — произвольная точка эллипса. Обозначим AF1 + AF2 = 2a. Проведем биссектрису с угла, смежного с углом F1AF2. Тогда углы, образованные этой прямой с отрезками AF1 и AF2 равны. Докажем, что прямая с будет касательной к эллипсу. Рассмотрим точку F′, симметричную точке F2 относительно прямой с. Она принадлежит прямой F1A и F1F′ = 2a. Для произвольной точки A′ прямой с, отличной от А, имеем A′F2 = A′F′, A′F1 + A′F2 = A′F1 + A′F′ > F1F′ = 2a. Следовательно, точка A′ не принадлежит эллипсу и прямая с имеет только одну общую точку А с эллипсом, т. е. является касательной.

Дальше

Свойства фокусов эллипса

Доказанное равенство углов можно интерпретировать следующим образом.
Если изготовить зеркальную поверхность в форме эллипсоида вращения — фигуры, полученной вращением эллипса вокруг его оси, и поместить в один из фокусов источник света, то лучи света, отразившись от зеркальной поверхности, соберутся в другом фокусе.
Слово «фокус» в переводе с латинского означает«очаг», «огонь», и именно это свойство эллипса по-служило основанием для названия точек F1, F2 фокусами.

Дальше

Парабола

Параболой (рис. 2) называ-ется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

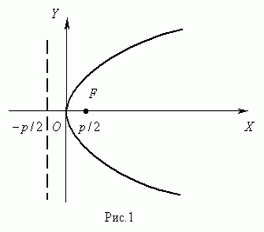
Рис. 2

Дальше

Парабола

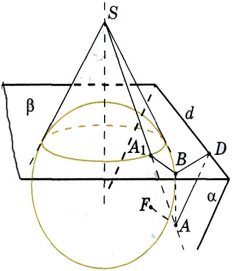
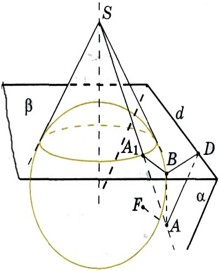
Выясним, что получится в сечении конической поверхности плоскостью а, если эта плоскость не проходит через вершину S и пересекает ось под углом φ, равным углу между образующей и осью конической поверхности. В этом случае одна из образующих будет параллельна плоскости сечения. Впишем в коническую поверхность сферу, касающуюся плоскости α в некоторой точке F и конической поверхности по окружности С, лежащей в плоскости р, перпендикулярной оси. Плоскости α и β образуют между собой угол 90º – φ и пересекаются по некоторой прямой d.

Дальше

Парабола

Пусть А — произвольная точка сечения. Проведем образующую АS и обозначим через A1 точку ее пересечения с окружностью С. Заметим, что прямая АS является касательной к сфере. Прямая АF также является касательной. Отрезки АF и АA1 равны как отрезки касательных, проведенных к сфере из одной точки. Опустим из точки А перпендикуляр АВ на плоскость β и перпендикуляр АD на прямую d. Угол A1АВ равен φ. Угол АОВ является углом между плоскостями α и β и поэтому равен 90º – φ. Следовательно, угол ВАО равен φ.