Конические сечения. Возможные сечения плоскостью, проходящей через вершину конической поверхности, страница 2

Пусть А (х, у) — точка плоскости, для которой расстояние до точки F равно расстоянию до прямой d. Выразим эти расстояния через координаты точки А. Получим равенство Возводя обе части этого равенства в квадрат и приводя подобные, имеем равенство 4ay = x2, которое является уравнением параболы. Точка F называется фокусом параболы, прямая d — директрисой параболы. Таким образом, парабола удовлетворяет следующему фокальному свойству: расстояние от произвольной точки параболы до ее фокуса равно расстоянию от этой точки до директрисы.

Дальше

Назад

Термины

• Осью параболы называется прямая, проходящая через фокус и перпендикулярная директрисе. Точка пересечения параболы с ее осью называется вершиной параболы.
• Определение. Прямая, имеющая с параболой только одну общую точку и не параллельная оси, называется касательной к параболе.
• Теорема. Углы, образованные касательной к параболе с ее осью и отрезком, соединяющим точку касания с фокусом, равны.

Дальше

Назад

Доказательство факта

Доказательство. Пусть задана парабола с фокусом F и директрисой d, А — произвольная точка параболы. Опустим из нее перпендикуляр АD на директрису. Проведем биссектрису угла FAD (рис. 3). Докажем, что соответствующая ей прямая а будет касательной к параболе. Действительно, точки F и О симметричны относительно прямой а. Из произвольной точки А' прямой а, отличной от А, опустим перпендикуляр А'D' на прямую d. Тогда A′F = A′D > A′D′. Это означает, что точка А' не принадлежит параболе и прямая а имеет только одну общую точку А с параболой, т. е. является касательной.

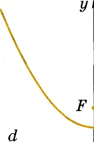
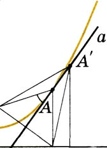
Рис. 3

Дальше

Назад

Гипербола

Гиперболой (рис. 4) назы-вается геометрическое место точек, модуль разности рас-стояний от которых до двух заданных точек  F1 и F2, назы-ваемых фокусами гипербо-лы, есть величина постоян-ная.

Дальше

Назад

Гипербола

Рассмотрим случай, когда плоскость сечения конической поверхности не проходит через вершину S и пересекает ось под углом, меньшим чем угол φ, между образующей и осью конической поверхности. В этом случае в сечении получается кривая, называемая гиперболой. Она состоит из двух частей, лежащих по разные стороны от вершины, называемых ветвями гиперболы. Для установления свойств гиперболы и ее уравнения впишем в коническую поверхность сферы, касающиеся плоскости сечения в некоторых точках F1 и F2 и конической поверхности по окружностям C1 и C2, лежащим в плоскостях, перпендикулярных оси.

Дальше

Назад

Гипербола

Пусть А — произвольная точка сечения. Предположим для определенности, что она лежит в той же части, что и точка F1. Проведем образующую АS и обозначим через A1, A2 точки ее пересечения с окружностями C1, C2, соответственно. Восполь-зуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF1 = AA1, AF2= AA2. Поэтому AF2 – AF1 = AA2 – AA1 = A1A2. Но длина отрезка A1A2 не зависит от выбора точки А сечения. Она равна сумме образующих соответ-ствующих конусов. Поэтому разность AF2 – AF1 расстояний от точки A до точек F1, F2 будет постоянной. Аналогично доказывается, что если точка A лежит в той же части, что и точка F2, то искомая разность будет равна первой.

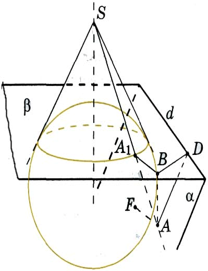
Дальше

Назад

Фокальное свойство

Таким образом, мы доказали, что для гиперболы выполняется следующее фокальное свой-ство: Модуль разности рассто-яний от произвольной точки гиперболы до двух данных точек, называемых фокусами, есть величина постоянная.

Дальше

Назад

Уравнение гиперболы

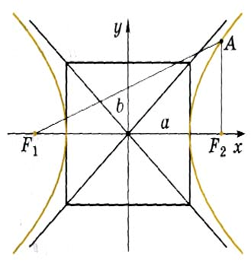
Используя фокальное свойство гиперболы, выведем ее уравнение. Пусть F1, F2 — фокусы гиперболы, А — точка на гиперболе. AF1 – AF2 = 2a, а > 0. Введем систему координат, считая осью абсцисс прямую, проходящую через фокусы, а осью ординат прямую, перпендикулярную оси абсцисс и делящую отрезок F1F2 пополам. Пусть фокусы имеют коорди-наты F1(–с, 0), F2 (с, 0), a < с. Точка А имеет координаты А (х, у).

Дальше

Назад

Уравнение гиперболы

Тогда , , и равенство можно переписать в виде Перенесем второй корень в правую часть и возведем все в квадрат. Получим . Раскрывая и приводя подобные члены, имеем равенство Еще раз возводя в квадрат и обозначая получим Разделив обе части уравнения на , окончательно получим уравнение гиперболы

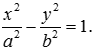
Дальше

Назад

Термины

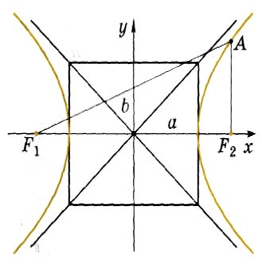
Изображенный на рисунке прямо-угольник называется асимптотическим прямоугольником гиперболы, а прямые, на которых лежат диагонали этого прямоугольника, называются асимп-тотами гиперболы. Число е = a/c называется эксцентриситетом гипер-болы. Определение. Прямая, не парал-лельная ни одной из асимптот и имеющая с гиперболой только одну общую точку, называется касательной к гиперболе.

Дальше

Назад

Контрольная работа

Итак, теперь, после ознакомления с теорией, вы готовы к написанию контрольной работы по пройденному материалу. Контрольная работа. Даны уравнения: 1. x2 + 9y2 = 1; 2. x2 – 9y2 = 1. Доказать, что уравнение (1) задает эллипс, а уравнение (2) — гиперболу. Построить их, найти асимптоты, эксцентриситеты, директрисы, фокусы, полуоси.

Назад

Дальше