











MAPLE
Первоначальное знакомство
Интерфейс пользователя
Исполняемые команды вводятся после специального приглашения '>', красным цветом и должны заканчиваться точкой с запятой или двоеточием. В одной строке может быть расположено более одной команды. Если после команды стоит двоеточие, то результат её выполнения не будет отображен на экране. Если же после команды стоит точка с запятой, то после её выполнения на экране появится результат. Если Maple не сможет вычислить введённое выражение, то результатом будет перевод введённого выражения в математический формат, принятый для вывода. Выходная информация печатается синим цветом. Исполнение Maple-команды инициируется нажатием ввода (Enter).
Работа с числами (часть 1)
1. Сложение и вычитание задаются знаками «+» и «–»: > 129140163+43046721–134217728; 37969156 2. Умножение задается символом «*»: > 29*15648; 453792 3. Возведение в степень задается символом «^»: > 2^100; 1267650600228229401496703205376
Работа с числами (часть 2)
4. Деление задается символом «/»: > 7/18+10/21 Обратите внимание, что Maple выполняет вычисления с абсолютной точностью. Если у числа поставить десятичную точку, то вычисления будут приближёнными: > 7./18+10/21; 0.8650793651 5. Вычисление факториала* задаётся символом «!»: > 20!; 2432902008176640000
![]()
* Факториалом натурального числа n называют произведение всех чисел от 1 до n: n! = 1·2·3·...·n
Работа с числами (часть 3)
6. Извлечение квадратного корня из числа x задаётся символами sqrt(x): > sqrt(11–6*sqrt(6)); > sqrt(–4); 2I Символом I в Maple обозначается мнимая единица . 7. Знак числа определяется функцией «sign»: > sign(–4); sign(3–sqrt(8)); –1 1
![]()
![]()
Константы и переменные (часть 1)
1. Для вычисления сложных выражений полезно производить промежуточные вычисления, присваивая их значения переменным. Имена переменным можно давать как латинские, так и греческие. Значения переменных меняются с помощью оператора присваивания «:=»: > phi:=Omega*t–k*r; Delta:=A*sin(phi); Обратите внимание, что Maple чувствителен к регистру. Переменные a и A — разные.
![]()
![]()
Константы и переменные (часть 2)
2. Число π обозначается «Pi», в отличие от греческих букв «pi» малыми буквами (это π) или «PI» большими буквами (это Π): > sin(2*pi/3)=sin(2*Pi/3); > tan(pi/4)=tan(Pi/4); Обратите внимание, что тангенс обозначается «tan», а не привычным «tg».
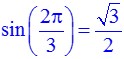
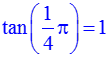
Константы и переменные (часть 3)
3. Мнимая единица обозначается символом «I»: > I^2; (1+I)^2; exp(i*pi)=exp(I*Pi); –1 2I 4. При попытке присвоить значение защищённой константе приведёт к ошибке: > 2:=1; Error, invalid left hand side of assignment
![]()
Преобразования и вычисления (часть 1)
1. Использование точных значений математических выражений не всегда удобно. Для их перевода в формат записи с плавающей точкой с одновременным округлением с указанной точностью используется функция evalf: > evalf(Pi,30); 3.14159265358979323846264338328 > sqrt(2)=evalf(sqrt(2),6);
![]()
Преобразования и вычисления (часть 2)
2. Для преобразования алгебраических выражений можно использовать: раскрытия скобок (expand), группировки (collect), разложения на множители (factor для многочленов и ifactor для целых чисел), упрощение выражений (simplify): > x^2–2*x*y+3*x^2*y–x*y^2+7=collect(x^2–2*x*y+3*x^2*y–x*y^2+7,y); x2 – 2xy + 3x2y – xy2 + 7 = –xy2 + (–2x + 3x2)y + x2 + 7 > (x^2–2*x+1)*(x^2+2*x+1)=expand((x^2–2*x+1)*(x^2+2*x+1)); (x2 – 2x + 1)(x2 + 2x + 1) = x4 – 2x2 + 1 > sin(4*x)=expand(sin(4*x)); sin(4x) = 8sin(x)cos(x)3 – 4sin(x)cos(x) > x^4–y^4=factor(x^4–y^4); x4 – y4 = (–y + x)(x + y)(x2 + y2) > ifactor(2^15+1); (3)2(11)(331) > a:=(y+x)^2–(y–x)^2; simplify(a); a := (x + y)2 – (y – x)2 4xy
Преобразования и вычисления (часть 3)
3. Наименьшее общее кратное чисел вычисляется с помощью «ilcm»: > ilcm(12,15); ilcm(12,15,7); 60 420 4. Наибольший общий делитель чисел вычисляется с помощью «igcd»: > igcd(12,15); igcd(12,15,7); 3 1
Примеры
1. Сравнить числа 2100 и 363: > sign(2^100–3^63); 1 т. к. знак разности равен 1, следовательно, первое число больше. 2. Вычислить tg(81º27’) с точностью до 0,001: > evalf(tan((81+27/60)*Pi/180),4); 6.671 3. Упростить выражение (a + b)4 – (a – b)4: > (a+b)^4–(a–b)^4=simplify((a+b)^4–(a–b)^4); (a + b)4 – (a – b)4 = 8a3b + 8ab3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.