Впервые экспериментально доказал существование электромагнитных волн Г. Герц, что послужило решающим толчком в признании электромагнитной природы света.
Следующим решающим шагом в понимании природы света явилось введение в начале 20 века Максом
Планком квантования энергии излучающих осцилляторов, после чего Эйнштейн применил планковскую идею квантования непосредственно к самому излучению. Впоследствии эти порции излучения стали называться фотонами.
3
Таким образом, современнаяфизика, говоря о «свете», стала подразумевать широкуюсовокупностьединыхпосвоейприродеявлений, сводящихсякраспространениюкороткихэлектромагнитныхволн, проявляющихкакволновые, такикорпускулярныесвойства.
4
2. ЭЛЕКТРОМАГНИТНАЯ ПРИРОДА СВЕТА. УРАВНЕНИЕ ЭЙКОНАЛА
Электромагнитные колебания, соответствующие видимой области спектра, происходят с частотами порядка ν = (4.7 ÷ 7.9) 1014 Гц, что соответствует длинам волн в диапазоне λ=(380÷780) нм. Поэтому при решении волнового уравнения для электромагнитных волн в первом приближении можно положитьλ<< l , где l – характерный размер оптических элементов.
В этом случае можно получить уравнение эйконала, которое позволяет строго обосновать физическую природу световых лучей, как разновидности электромагнитного излучения, и определить с одной стороны ограничения, связанные с приближением геометрической оптики (λ→0), а с другой стороны, обосновать принципы волновой оптики, учитывающие конечность длины волны.
Для любой компоненты электромагнитного поля в непоглощающей среде выполняется волновое уравнение:
∆Ψ
-
(1
υ2)∂2Ψ
∂t2
=
0,
(1) r r
где под Ψ подразумеваются векторы Eили H , υ - скорость
распространения электромагнитной волны в среде,
-
оператор Лапласа.
r Для монохроматических волн Ψ(r,t) можно представить в виде:
5
r r
Ψ(r,t)=ψ(r)exp(−ωt). (2)
Подставляя (2) в (1), получаем уравнениеr для зависящей только от координаты амплитуды ψ(r):
ω2
∆ψ+ 2ψ= 0, υ
∆ψ+ n2k02ψ= 0 , (3)
где k0
=ωc - волновое
число для вакуума, n - показатель преломления среды.
Далее, чисто формально, проведём двойное дифференцирование по ∂x функции lnψ(x), и получим тождество (формулулогарифмическогодифференцирования, которая необходима для преобразования волнового уравнения к удобному для наших целей виду):
ψ
∂2x2 =∂x22 (lnψ)+ (lnψ)2 . (4) ∂x
Аналогичные выражения получаются для производных по y и z.
Применяя тождество (4) уравнение (3) можно преобразовать к виду:
6
∆(lnψ)+ [grad(lnψ)]2 + n2k02 = 0. (5)
По аналогии с решением волнового уравнения в виде плоской волны, распространяющейся в среде с r
показателем преломления n , представим ψ(r) в виде:
( )rr eik0ϕ( )rr (6) ψ= A
r
где ϕ(r) - скалярная вещественная функция от координат, называемая эйконалом, а амплитуда Aзависит от положения рассматриваемой точки.
Поставляя выражение (6) в уравнение (5) и деля на k02, получаем:
∆ln A [grad(ln A)]2 i(∆ϕ+2grad(ln A)gradϕ)
2 + 2 +
k0 k0 k0 (7)
[gradϕ]2 +n2 = 0
Первое и второе слагаемые имеют порядок величины
∆ln A+[grad(ln A)]2 1 ∂2A ∂2A ∂2A
k
,
λ2
A ~ 
2 k0
A l
где l - характерная длина, на которой амплитуда A
7
волны изменяется существенно. Величина l определяется размерами оптических элементов: линз, диафрагм и т.д. Для оптического диапазона длин волн l >>λ . Тогда первым слагаемым в уравнении (7) можно пренебречь.
Приравнивая нулю действительную и мнимую части уравнения (7), получаём для действительной части
[grad ϕ(rr)]2 = n2, или
r r
grad ϕ(r)= ns , (8)
r
где s - единичный векторr , направленный перпендикулярно к поверхности ϕ(r)= const .
r
Функция ϕ(r) называется функциейэйконала, а выражение (8) - уравнениемэйконала.
8
Раздел оптики, в котором пренебрегают конечным значением длин волн, носит названиегеометрическойоптики.
То есть геометрическаяоптикаявляетсяприближённымпредельнымслучаем, вкоторыйпереходитволноваяоптика, когдадлинаволнысветаλ→0.
Геометрическая оптика использует представление о световых лучах - линиях, вдоль которых происходит распространение энергии световых колебаний. Пучки света рассматриваются как совокупности бесконечного числа независимых лучей, удовлетворяющих законам прямолинейного распространения в однородной среде, зеркального отражения и преломления на границе раздела двух сред.
Многие простые оптические явления
(возникновение теней, образование изображений в оптических приборах) можно объяснить на основе законов геометрической (лучевой) оптики.
Уравнение эйконала является основным уравнением геометрической оптики, а его вывод определяет ограничения по его использованию.
Первым ограничением (условием) применимости законов геометрической оптики является малость изменения амплитуды волны и её первых
9
пространственных производных на протяжении длины волны (связано с тем, что при выводе уравнения эйконала предполагалось, что первые два слагаемые малы по сравнению с остальными). То есть законы геометрической оптики не применимы для областей, в которых велики пространственные производные амплитуды волны, например, для фокальной плоскости линзы, где поле концентрируется в точке, и его производная бесконечна велика.
Второе ограничение связано с тем, что в волновом уравнении (1) полагается n = const, то есть ε= const,µ= const . То есть законы геометрической оптики не применимы для областей с резкими изменениями характеристик среды, например, края линзы или экрана, где нельзя не учитывать дифракционные явления.
r
Поверхность, для которой ϕ(r)= const , называется геометрической волновой поверхностью или геометрическим волновым фронтом.
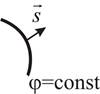
Рис.1
r
Вектор s показывает направление распространения светового луча в каждой точке волнового фронта (рис. 1).
Лучомназываютлинию, касательнаяккаждойrточкекоторойсовпадает
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
