Формула Планка и квантование энергии излучения. Стоячие волны в полости - модели чёрного тела. Формула Рэлея-Джинса

области наблюдаются узлы, уравнения (1) выглядят следующим образом:

 

Сложение колебаний ξ₁ и ξ₂ в случае пучностей на границах приводит к уравнению

                 (2) и в случае узлов на границах — к уравнению

             (3) 

Для того чтобы и на другой границе (т. е. при х = а) наблюдалась пучность (в случае, описываемом уравнением (2)) либо узел (в случае, описываемом уравнением (3)), необходимо, чтобы произведение ka было целым кратным π: 

ka=nπ.

Таким образом, независимо от того, что наблюдается на границах области (пучности или узлы), модуль волнового вектора должен иметь значения

                            (4)

Отсюда следует

a

n= k                                                 (5) π

Из (5) следует, что  в интервале значений волнового вектора ∆k число стоячих волн ∆N_k равно

 

4

Значения N_k образуют дискретную последовательность. Заменив эту последовательность непрерывной функцией, можно  написать

                                    (6)

Модуль волнового вектора связан с частотой ω и скоростью v соотношением

                                        (7)

Соответственно

                                   (8)

(мы считаем, что дисперсии нет, т. е. v = const). 

Заменив в (6) dk через dωv, придём к формуле 

                           (9) где dN_ω— число стоячих волн, частоты которых лежат в интервале от (ω до ω+dω).

   Теперь рассмотрим трёхмерный случай, рис. 2.

 

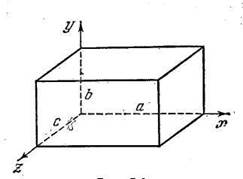
Рис. 2.

5

По аналогии с формулой (4) на долю каждой точки приходится объем 

π3 π3

= abc   V (V — объем области). 

Число стоячих волн, у которых проекции волновых векторов заключены в пределах от k_x до k_x + dk_x, от k_y до k_y + dk_y и от k_z до k + dk_z, определяется по аналогии с (6) выражением

                     (10)

В k -пространстве с осями k_x, k_y, k_z каждой стоячей волне отвечает точка в первом октанте (рис. 3). 

 

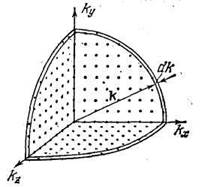
Рис. 3.

Число стоячих волн, у которых модуль волнового вектора лежит в пределах от k до k + dk, равно количеству точек, попадающих в пределы 1/8 шарового слоя радиуса k

и толщины dk (см. рис. 3). Следовательно

                  (11)

6

Приняв во внимание формулы (7) и (8), получим число стоячих волн, частоты которых попадают в интервал от ω до ω+ dω:

                           (12)

Выражение (12) пропорционально объему полости V. Поэтому можно говорить  о  числе стоячих  волн dn_ω,  приходящихся на единицу объёма полости. Это число равно (для одной поляризации света): 

                             (13)

Таким образом, формула (13) задаёт число осцилляторов dn_ω чёрного тела единичного объёма, излучающих в полосе

частот dω на произвольной частоте ω.

7

2.  ФОРМУЛА РЭЛЕЯ-ДЖИНСА

Рэлей подошел (1900) к изучению спектральных закономерностей черного излучения с позиций статистической физики, а не термодинамики, как это делали его предшественники. Он рассмотрел равновесное (черное) излучение в замкнутой полости с зеркальными стенками как совокупность пространственных стоячих электромагнитных волн. Частоты этих волн должны удовлетворять определенным условиям, подобным условиям для частот стоячих упругих волн в стержнях. Рэлей показал, что число dnтаких собственныхчастот, находящихся в интервале от v до v + dv, пропорционально объему полости V, квадрату частоты v и ширине интервала dv: 

dn ~ Vv²dv.

Колебания с разными собственными частотами совершаются независимо друг от друга. Каждой собственной частоте соответствует своя колебательная степень свободы черного излучения. Применив закон классической статистической физики о равном распределении энергии по всем степеням свободы равновесной системы, Рэлей показал, что энергия d W излучения в полости, соответствующая интервалу частот от v до v + dv,

 

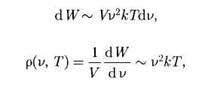
8

где кТ — средняя энергия, приходящаяся на одну колебательную степень свободы. Таким образом, Рэлей получил, что

 

В дальнейшем Рэлей и Джинс уточнили эту формулу, вычислив значение коэффициента пропорциональности:

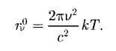                             (14)

Формула Рэлея —Джинса(14) хорошо согласовалась с данными опытов только в области малых частот излучения (кривая 1; рис. 4). 

 

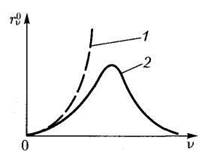
Рис. 4.

Для больших частот она была явно неверна (кривая 2). Формула Рэлея —Джинса противоречила также закону смещения Вина и закону Стефана —Больцмана: по формуле (14) r_ν⁰ монотонно возрастает с ростом частоты, не имея максимума, а R_э⁰ при любой температуре обращается в бесконечность:

9

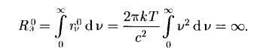                 (15)

Работы Рэлея и Джинса показали, что последовательное применение классическойфизики к исследованию спектрального состава черного излучения дает абсурдные результаты, находящиеся в противоречии с законом сохранения энергии.

Невозможность отыскания методами классической теоретической физики такого выражения для функции Кирхгофа, которое согласовывалось бы с данными эксперимен тов во всем интервале частот от 0 до ∞, получило образное название «ультрафиолетовой катастрофы». (Смысл названия заключается в том, что нарушение закона сохранения энергии происходит при подстановке в интеграл (15) бесконечности в качестве верхнего «ультрафиолетового» предела частот).

10

3. ФОРМУЛА ПЛАНКА

Найти правильное выражение для функции Кирхгофа и дать теоретическое обоснование спектральным закономерностям черного излучения впервые удалось немецкому физику М. Планку. 

Выше уже отмечалось, что объемная плотность энергии равновесного излучения в замкнутой полости и распределение энергии этого излучения по частотам зависят только от температуры стенок полости. Материал стенок, т.е. конкретные свойства системы, с которой связано равновесное излучение, не играет никакой роли. 

В своих расчетах Планк выбрал наиболее простую модель излучающей системы (стенок полости) в виде совокупности линейных гармонических осцилляторов (электрических диполей) со всевозможными собственными частотами ν (см. предыдущий раздел о стоячих волнах). 

Исходя из того, что в состоянии термодинамического равновесия расход энергии на излучение осцилляторов с собственной частотой v должен полностью компенсироваться в результате поглощения этими осцилляторами энергии падающего на них излучения, Планк показал (1899), что

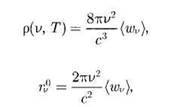                            (16) 

11

где (w_v) — средняя энергия осциллятора с собственной частотой v. 

Если бы для ее определения Планк, подобно Рэлею, воспользовался законом классической статистической физики о равном распределении энергии по всем степеням свободы равновесной системы, то он получил бы, что (w_v) = kT. При этом его формула (15) совпала бы с формулой Релея-Джинса (14). 

Однако Планк пытался найти выражение для (w_v), исходя из термодинамических соотношений. Он был убежден, что между энтропией S осциллятора и его средней энергией должна существовать сравнительно простая связь.

В октябре 1900 г. Планку удалось подобрать такой вид зависимости  w

                  (17) где а₁и а₂ — постоянные коэффициенты.

Оказалось, что формула (17) хорошо согласуется с результатами