Волновая поверхность падаю щей волны, плоскость щели и экран параллельны друг другу.
Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому достаточно исследовать характер картины в одной такой плоскости, например в плоскости 2
рис. 1. Все вводимые в дальнейшем величины, в частности угол ϕ , образуемый лучом с оптической осью линзы, относятся к этой плоскости.
Разобьем открытую часть волновой поверхности на параллельные краям щели элементарные зоны ширины dx. Вторичные волны, посылаемые зонами в направлении, определяемом углом ϕ , соберутся в точке экрана Р.
Каждая элементарная зона создаст
в точке Рколебание
dE. Линза собирает в фокальной
плоскости плоские (а несферические)
волны. Поэтому множитель 1r в выражении (1, лекции 6) для dE в случае дифракции Фраунгофера будет отсутствовать. Ограничившись рассмотрением не слишком
больших углов ϕ , можно коэффициент Кв
формуле (1, лекции 6) считать постоянным. Тогда амплитуда колебания, возбуждаемого зоной в любой
точке экрана, будет зависеть только от площади
зоны. Площадь пропорциональна ширине зоны dx. Следовательно, амплитуда dA колебания dE, возбуждаемого зоной ширины dx в любой точке экрана, имеет вид
где С — константа.
Обозначим алгебраическую сумму амплитуд колебаний, возбуждаемых в некоторой точке экрана всеми зонами, через A0 . Ее можно найти, проинтегрировав dA по всей ширине щели b :
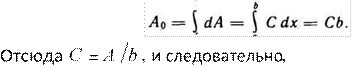
0
3
Теперь определим фазовые соотношения между колебаниями dE. Сопоставим фазы колебаний, возбуждаемых в точке Рэлементарными зонами с координатами Оих(рис. 1). Оптические пути ОРи QP таутохронны, поэтому разность фаз между рассматриваемыми колебаниями образуется на пути ∆, равном xsin ϕ. Если начальную фазу колебания, возбуждаемого в точке Рэлементарной зоной, находящейся в середине щели (х = 0), положить равной нулю, то начальная фаза колебания, возбуждаемого зоной с координатой х, будет равна
(λ— длина волны в данной среде).
Таким образом, колебание, возбуждаемое элементарной зоной с координатой хв точке Р(положение которой определяется углом ϕ ), может быть представлено в виде
(1)
(имеется в виду вещественная часть этого выражения). Проинтегрировав выражение (1) по всей ширине щели, найдем результирующее колебание, возбуждаемое в точке Роткрываемым щелью участком волновой поверхности:
.
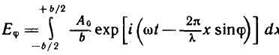Вынесем множители, не зависящие от х, за знак интеграла. Кроме того, введем обозначение
4
(2)
В результате получим
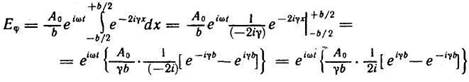
Выражение в фигурных скобках определяет
)
комплексную амплитуду Aϕ результирующего колебания. Приняв во внимание, что разность экспонент, деленная на2i, представляет собой sin γb , можно написать
(3)
(мы подставили значение (2) для γ ).
Выражение (3) является вещественным. Его модуль представляет собой обычную амплитуду результирующего колебания:
(4)
Для точки, лежащей против центра линзы, ϕ= 0 .
Подстановка этого значения в формулу (4) дает для амплитуды значение Ао2.
При значениях ϕ , удовлетворяющих условию:
(5) амплитуда
Av обращается
в нуль.
5
Таким образом, условие (5) определяет положения минимумовинтенсивности.
Отметим, что bsin ϕ представляет собой разность хода ∆ лучей, идущих в точку Рот краев щели (см. рис.1).
Интенсивность света пропорциональна квадрату амплитуды. Следовательно, в соответствии с (4)
(6) где
I0— интенсивность в середине
дифракционной картины (против центра линзы; Iϕ—интенсивность в точке,
положение которой определяется данным значением ϕ .
Типичный график функции (6) изображен рис. 2.
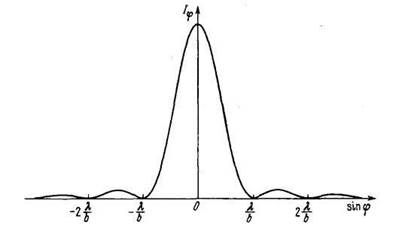
Рис. 2.
Из формулы (6) получается, что I−ϕ = Iϕ. Это означает, что дифракционная картина симметрична от-
6
носительно центра линзы. Заметим, что при смещении щели параллельно экрану (вдоль оси хна рис. 1)дифракционная картина, наблюдаемая на экране, остается неподвижной (ее середина лежит против центра линзы). Напротив, смещение линзы при неподвижной щели сопровождается таким же смещением картины на экране.
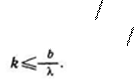Количество минимумов интенсивности определяется отношением ширины щели b к
длине волныλ.
Из условия (5) следует, что sinϕ=±kλ
b. Модуль sinϕне
может превысить единицу. Поэтому kλ b ≤1, откуда
(7)
Приширинещели, меньшейдлиныволны, минимумывообщеневозникают. В этом случае интенсивность света монотонно убывает от середины картины к ее краям.
Краям центрального максимума соответствуют значения угла ϕ , получающиеся из условия bsin ϕ=±λ. Эти значения равны ±arcsin(λ b). Следовательно, угловая ширина центрального максимума равна
(8)
В случае,
когда b >>λ , значение sin(λb)можно положить равнымλ b.
Тогда формула для угловой
ширины центрального максимума упрощается следующим образом:
(9)
7
Рассмотрим случай, когда ширина щели очень мала по сравнению с расстоянием от щели до экрана, а лучи, идущие в точку Рот краев щели, будут практически параллельными и в отсутствие линзы между щелью и экраном, рис. 3.
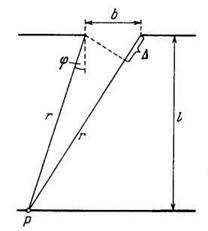рис. 3.
Следовательно, при падении на щель плоской волны будет наблюдаться дифракция Фраунгофера. Все полученные выше формулы будут справедливыми, причем под ϕ в этих формулах следует понимать угол между направлением от любого края щели к точке Ри нормалью к плоскости щели.
Установим количественный критерий, позволяющий определить, какой вид дифракции будет иметь место в каждом конкретном случае. Найдем разность хода лучей от краев щели до точки Р(рис. 3). Применим теорему косинусов к треугольнику со сторонами r , r+λ и b :
8
После несложных преобразований получим
(10)
Нас интересует случай, когда лучи, идущие от краёв щели в точку P, почти параллельны. При этом условии ∆2 << r∆, поэтому в уравнении (10) можно пренебречь слагаемым ∆2. В этом приближении
(11)
В пределе при r →∞получается значение разности хода
∆∞ = bsinϕ, (12) совпадающее с выражением, фигурирующим в формуле
(5).
При конечных r характер дифракционной картины будет определяться соотношением между разностью ∆−∆∞ и длиной волны λ. Если
(13) дифракционная
картина будет практически такой, как в
случае дифракции Фраунгофера.
При ∆ −∆∞, сравнимой с λ, т.е. если ∆ −∆∞ ~ λ , будет иметь место дифракция Френеля.
Из (11) следует, что
(l— расстояние от щели до экрана). Подстановка этого выражения в (13) приводит к условию:
9
(14)
Таким образом, характер дифракции зависит от значения безразмерного параметра, который носит название «ЧислоФренеля»:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
