Высказывания как форма мышления. Понятие, структура и виды простых высказываний. Отношения простых высказываний. Логический квадрат

Структура данного вида высказываний может быть представлена таким образом: “Некоторые S суть P ”, а в символической логике оно выражается формулой $х (P(х) Ù Q(х)) (читается: “Существует х, обладающий одновременно свойствами P и Q”). Частноутвердительные высказывания обозначаются буквой «I».

Общеотрицательныминазываются высказывания, являющиеся одновременно общими по количеству и отрицательными по качеству. Например, “Ни одно из предложенных решений не было удовлетворительным”. Структура общеотрицательных высказываний имеет вид “Ни одно S не суть P ”, а символически оно выражается формулой " х (P(х) → ØQ(х)) (читается : “Для всякого х верно, что если он обладает свойством P, то он не обладает свойством Q”). Данный вид высказываний принято обозначать буквой «E».

Частноотрицательныминазываются высказывания, являющиеся одновременно частными по количеству и отрицательными по качеству. Например, “Некоторые произведения современных английских прозаиков не переведены на русский язык”. Обобщённой схемой построения данного вида суждений является “Некоторые S не суть P ”, а в виде формулы оно выражается следующим образом: $х (P(х) Ù ØQ(х)) (читается: “Существуют такие х, которые обладают свойством P и не обладают свойством Q”). Частноотрицательные высказывания обозначают буквой «O»

3) Всю совокупность высказываний можно разделить на сравнимые и несравнимые высказывания. Сравнимыми считаются: а) простые высказывания, имеющие в своей структуре одинаковые по содержанию термины (субъект и предикат); б) сложные высказывания, в которых имеется хотя бы одно одинаковое простое высказывание. В противном случае высказывания несравнимы. Сравнимыми, например, будут высказывания “Все студенты нашего курса изучают логику” и “Некоторые студенты нашего курса изучают логику”, как и высказывания, выражаемые формулами p Ù (q Ù r) и r → (p Ú q). Высказывания «Все планеты светят отраженным светом» и «Париж — столица Франции», а также выражаемые формулами  q Ú r и p Ù Øs являются несравнимыми.

Сравнимые высказывания подразделяют на совместимые и несовместимые. Совместимость высказываний бывает трех видов: равнозначность, подчинение и частичное совпадение. Рассмотрим их подробнее. О равнозначности сложных высказываний говорилось выше в связи с анализом равносильных формул.

Отношение подчинения между высказываниями означает, что при истинности подчиняющего высказывания истинным является и подчиненное ему высказывание, в то время как обратное не всегда имеет место. Общее высказывание вида А (соответственно Е) подчиняет себе высказывание вида J (соответственно О).

Отношение частичного совпадения, или подпротивность, означает, что наряду с тем, что два находящихся в нем высказывания могут быть одновременно истинными, они могут принимать и несовпадающие значения (одно — истинно, другое — ложно, или наоборот), но не могут быть одновременно ложными. Например, не могут быть одновременно ложными высказывания, выражающимися формулами p Ú q и Øp Ú q. Отношение частичного совпадения имеет место между частноутвердительными (J) и  частноотрицательными (О) высказываниями.

Среди несовместимых отношений следует выделить, прежде всего, отношения противности и противоречия. Отношения противности означает, что два находящихся в нем высказывания не могут быть одновременно истинными, но могут быть одновременно ложными. С помощью таблиц истинности достаточно легко обосновать, что формулы (и, следовательно, выражаемые ими сложные высказывания) p Ù q и Øp Ù q не являются одновременно истинными, хотя и могут быть одновременно ложными. В отношении противности находятся одинаковые по количеству, но разные по качеству высказывания, то есть общеутвердительные (А) и общеотрицательные (Е).

Противоречащиминазываются высказывания, которые не могут быть ни одновременно истинными, ни одновременно ложными. В случае сложных высказываний противоречие выражается взаимоотрицающими и взаимодополняющими высказываниями. Что же касается противоречащих друг другу простых высказываний, то они отличаются друг от друга, как своим количеством, так и качеством. В отношении противоречия попарно находятся общеутвердительные (А) и частноотрицательные (О), а так

же общеотрицательные (Е) и частноутвердительные (J) высказывания.

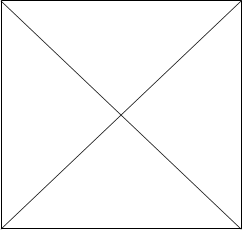Рис.

Отношения между простыми высказываниями иллюстрируются с помощью модели, получившей название «логический квадрат». По углам «логического квадрата»  (рис.) строго определенным образом расположены названия различных