При выполнении задачи № 5 необходимо использовать метод секущих плоскостей, сущность которого заключается в том, что для построения линии пересечения поверхностей геометрических тел необходимо подбирать дважды проецирующие секущие плоскости, т. е. плоскости параллельные или плоскости Н или плоскости V. Но, эти плоскости должны быть выбраны так, чтобы каждая секущая плоскость рассекла каждое геометрическое тело на простые плоские геометрические фигуры: окружности, треугольники, квадраты, прямоугольники. Там, где взаимно пересекутся эти плоские геометрические фигуры, там искомые точки линии пересечения.
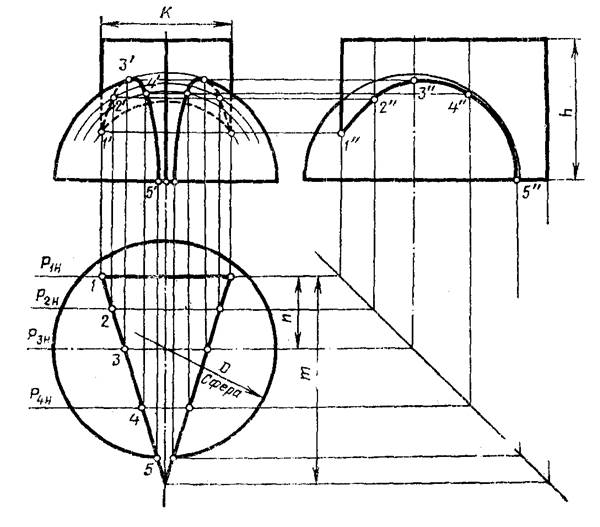
Рисунок 10 - Пример выполнения задачи № 5
Пример использования метода секущих плоскостей показан на рисунке 11.
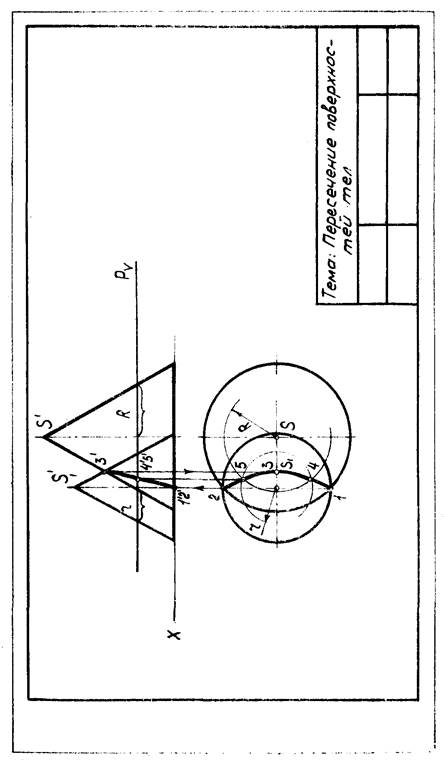 |
Рисунок 11 - Пример выполнения задачи № 5
План решения задач методом секущих плоскостей
1. Внимательно изучается чертеж и определяется, какие пересекаются геометрические тела.
В нашем случае два конуса.
2. Из чертежа определяется, нет ли уже готовых точек линии пересечения
В нашем случае есть — точки 1, 2 и 3'.
3. Определяем, какие секущие плоскости будем применять.
В нашем случае плоскость Р параллельную плоскости Н, т. к. она будет рассекать два конуса на окружности радиусов R и г. Там, где на горизонтальной проекции, в нашем случае, эти окружности пересекутся, там еще искомые точки 4 и 5. Находим их фронтальные проекции.
4. Последовательно проводим через точки лекальную кривую линии пересечения поверхностей геометрических тел.
Задача № 6. Тема: Взаимное пересечение поверхностей геометрических тел.
Для решения этой задачи необходимо применять метод секущих сфер.
Даны взаимнопересекающиеся поверхности геометрических тел.
Необходимо построить линии пересечения поверхностей геометрических тел.
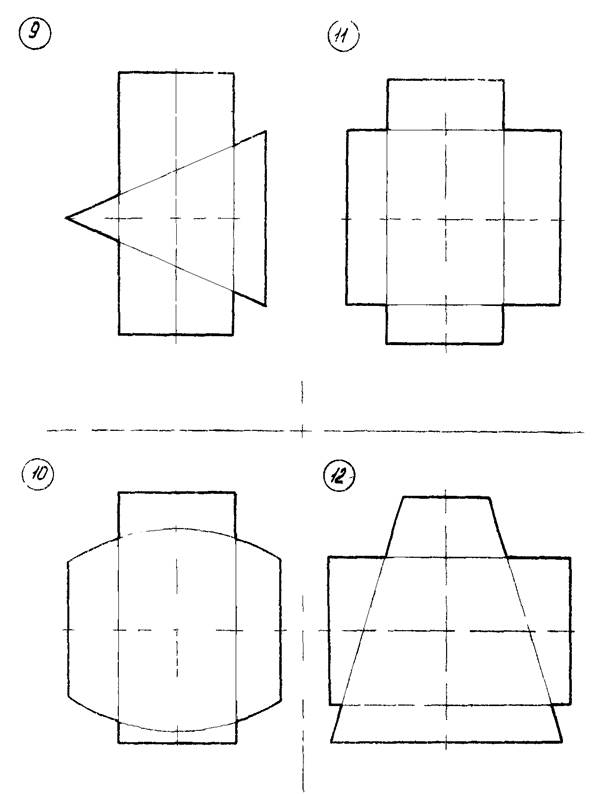
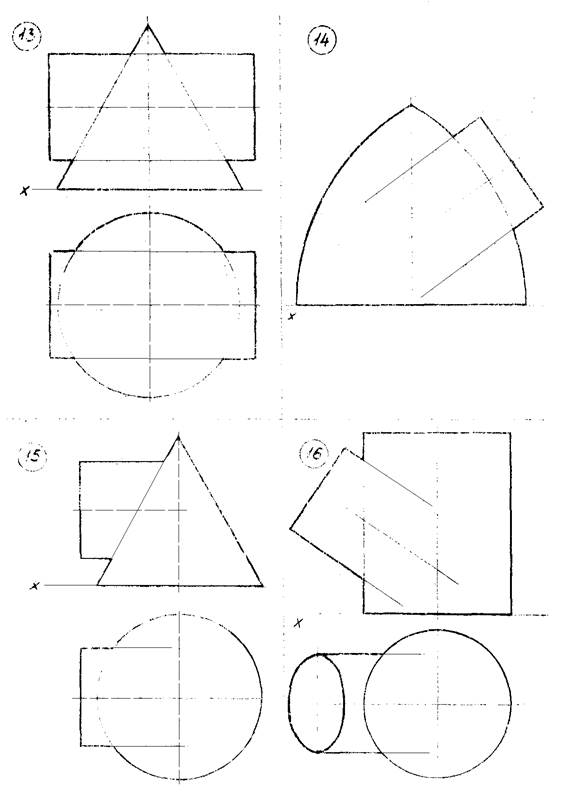
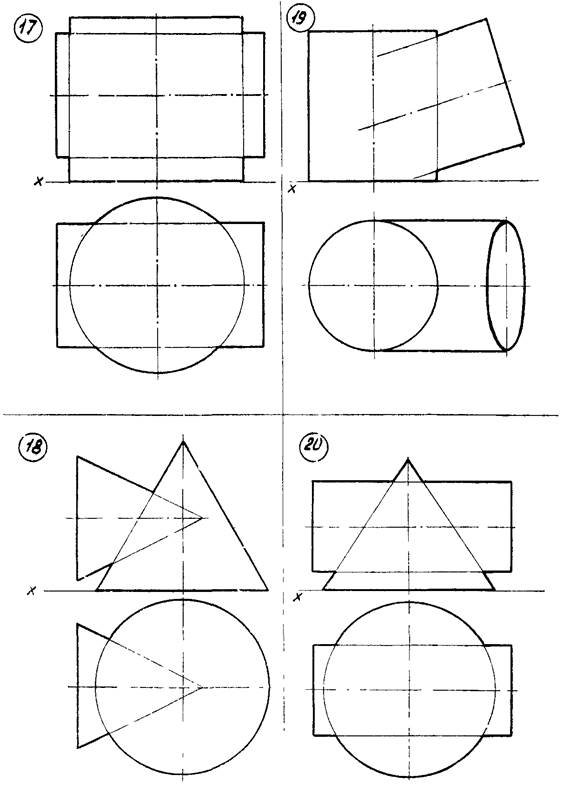
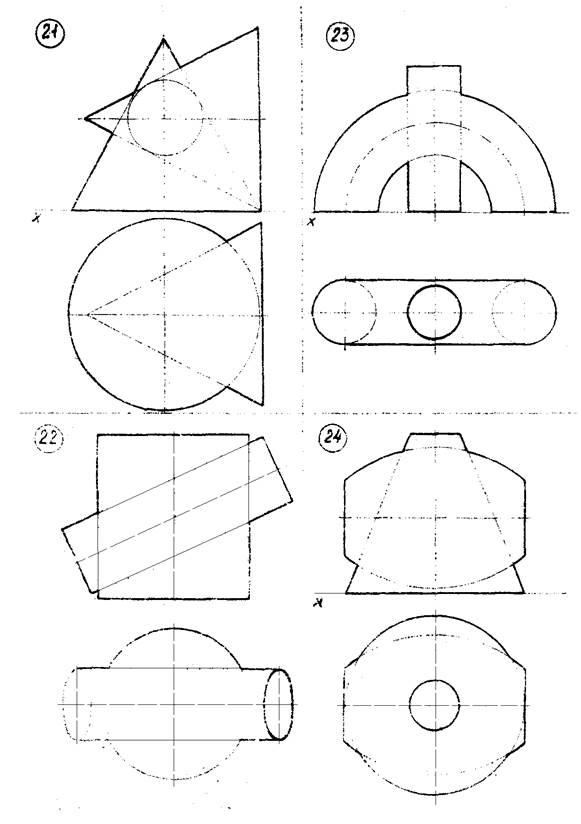
Варианты задач указаны на рисунке 12 (стр. 38…45).
Указания к выполнению задачи № 6
При решении этой задачи применяется метод секущих сфер, сущность которого заключается в том, что вписываемые сферы из центра пересечения осей симметрии геометрических тел обладают свойством мысленно рассекать себя и касающуюся поверхность какого-то тела на определенные окружности. Там, где окружности обоих геометрических тел взаимно пересеклись, там искомые точки линии пересечения. Как правило, вписывают две сферы, одну касательную к поверхности большего тела, а вторую несколько больше первой.
Покажем на рисунке 13, как пользоваться методом секущих сфер.
Пример выполнения показан на рисунке 14.
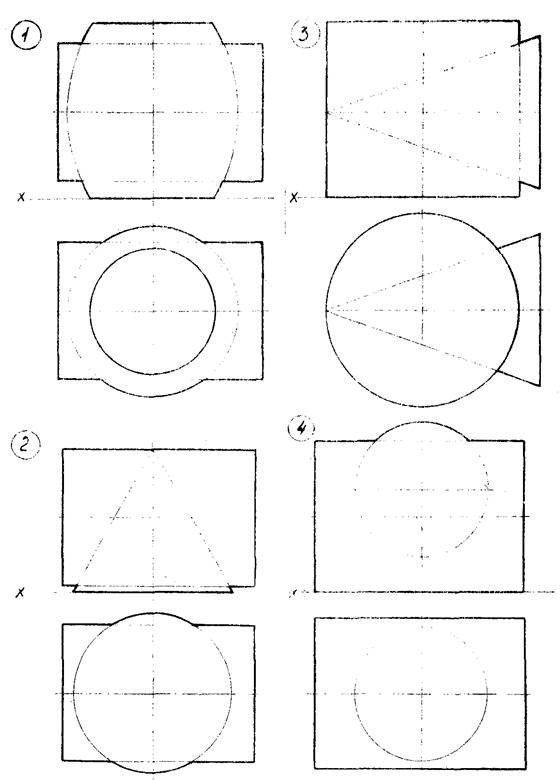
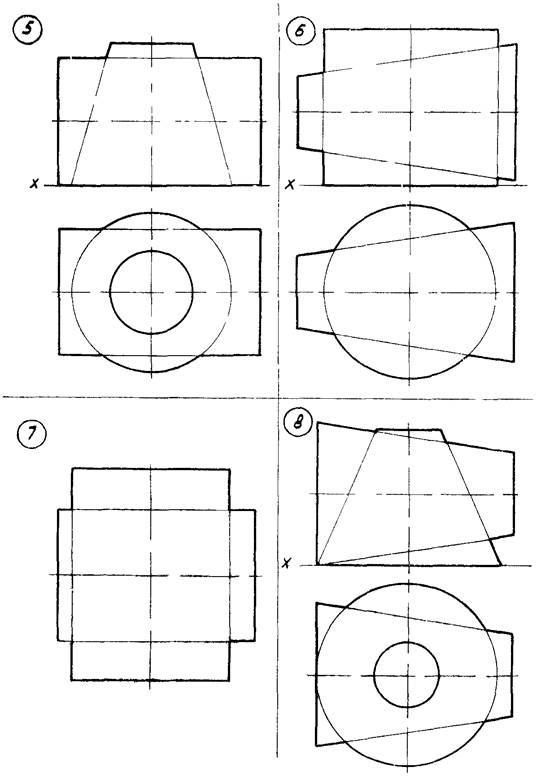
![]()
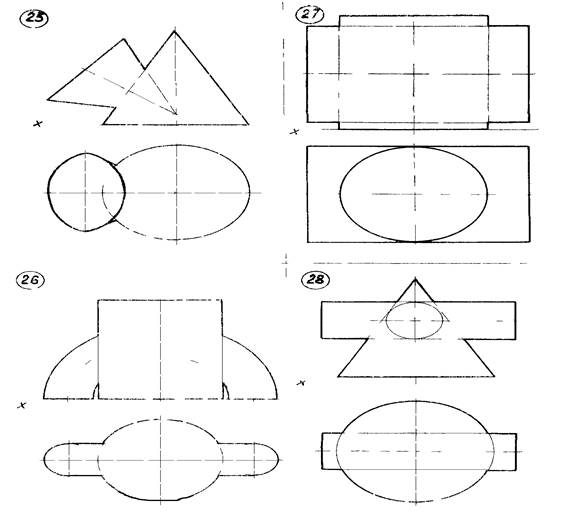
Рисунок 12 – Данные к задаче 6
План решения задачи № 6
1. Внимательно изучается чертеж и определяется, какие геометрические тела пересекаются.
В нашем случае два цилиндра.
2.По чертежу определяется, нет ли уже готовых точек линии пересечения. В нашем случае это точки 1' и 2'.
3. Из центра О' вписываем касательную сферу к большому цилиндру. Сфера рассекла себя и большой цилиндр по окружности a' a'; одновременно сфера рассекла себя и меньший цилиндр по окружности b'b'. Там, где окружность а'а' пересеклась с окружностью b'b', там две искомые точки 3' и 4'.
4. Из центра О' проводится еще одна сфера несколько большег диаметра, но нe больше размера 0'1'. Большая сфера пересекла себя и большой цилиндр по окружностям с'с' и d'd'. Большая сфера пересекла себя и меньший цилиндр по окружности е'е'. Там, где окружности с'с' и d'd' пересеклись с окружностью е'е', там точки 5', 6', 7', 8'.
5. Выполняем лекальную кривую линии пересечения.
6. Последовательно находим горизонтальные проекции точек 1, 2, 3, 4, 5, 6, 7, 8 линии пересечения и строим горизонтальную проекцию линии пересечения.
![]()
Рисунок 12 – Использование метода секущих сфер
![]()
Рисунок 13 - Пример выполнения задачи №6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.