2. Плоскость Р пересекает плоскость ABC по линии 1'2'. Находим горизонтальную проекцию линии пересечения 12, для этого находим на стороне ab точку 1, а на ас точку 2.
3. Там, где линия 12 отсекает dк, там точка m встречи прямой DK с плоскостью ABC. По линии проекционной связи находим на d'к' точку m'.
4. Заключаем еще прямую АВ в горизонтально-проецирующую плоскость Q (плоскость Q перпендикулярную горизонтальной плоскости проекций Н). На эпюре горизонтальный след QH сливается с ab.
5. Плоскость Q пересекает треугольник DEK по линии 34. Находим фронтальную проекцию линии пересечения 3'4', для этого находим на стороне ED точку 3' и на стороне ЕК точку 4'.
6. Там, где линия 3'4' отсекает прямую АВ, там точка n' встречи прямой АВ с плоскостью ЕДК.
7. Соединяем точки n' и m' и n и m. Это и будет две проекции линии пересечения треугольников.
8. Видимость на эпюре определяется, как выше описано на рисунке 4.
План решения задачи № 3 (вторая задача)
1. Вычерчиваем по своим координатам треугольник ABC.
2. Выполняем построение новой горизонтальной проекции (копию) с abc, но так, чтобы ГПГ плоскости ABC была перпендикулярна к оси X. Тогда треугольник ABC станет фронтально-проецирующей, т. е. перпендикулярной плоскости V. Для этого в плоскости ABC проводим горизонталь. На эпюре это с'5' и с5. Через точку с проводим ось 00 перпендикулярно плоскости Н. Вокруг 00 повернем треугольник так, чтобы ГПГ стала перпендикулярно оси X. На фронтальной плоскости точки а' и b' будут описывать дуги, параллельные оси X. При первом вращении треугольника фронтальная проекция спроецируется в линию a'lb'1c'.
3. Второе вращение произведем вокруг оси 00, перпендикулярной плоскости V и проходящей через точку b'1. Но повернем треугольник так, чтобы он стал параллельным плоскости Н. На эпюре проекция Ь'1с'2а'2 должна быть параллельна оси X. На горизонтальной проекции точки a1 и с опишут дуги параллельные оси X.
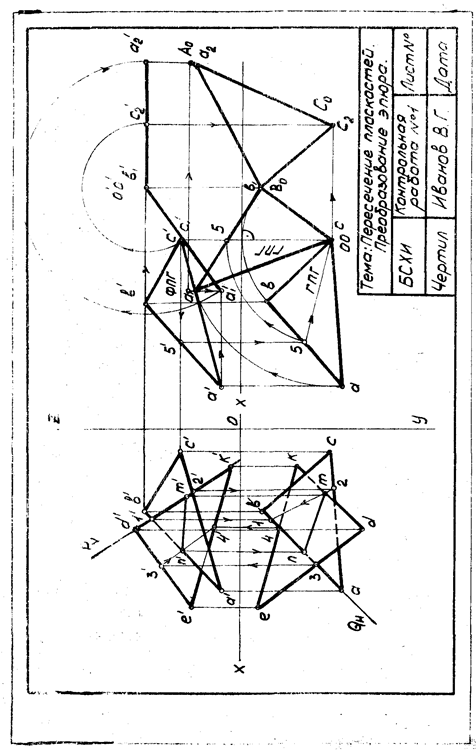
Рисунок 5 - Пример выполнения задачи № 3
Задача № 4. Тема: Пересечение геометрических тел плоскостью.
Даны геометрические тела: призма, пирамида, цилиндр и конус.
Для выполнения этой задачи студент выбирает по своему усмотрению по своему варианту одно из двух указанных геометрических тел на рисунке 6 (стр. 17…24).
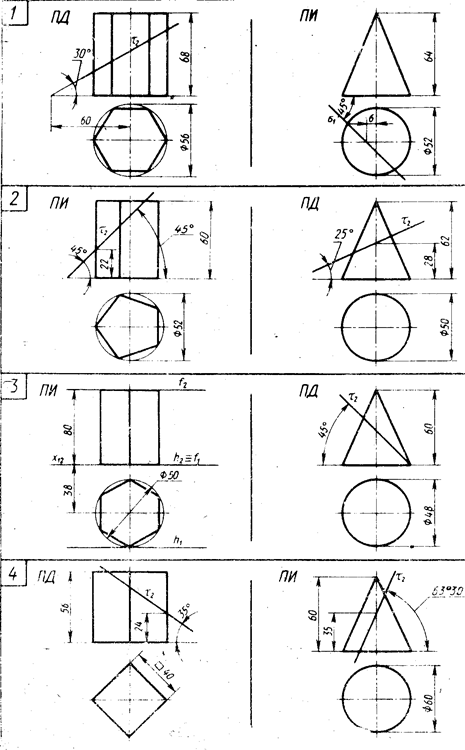
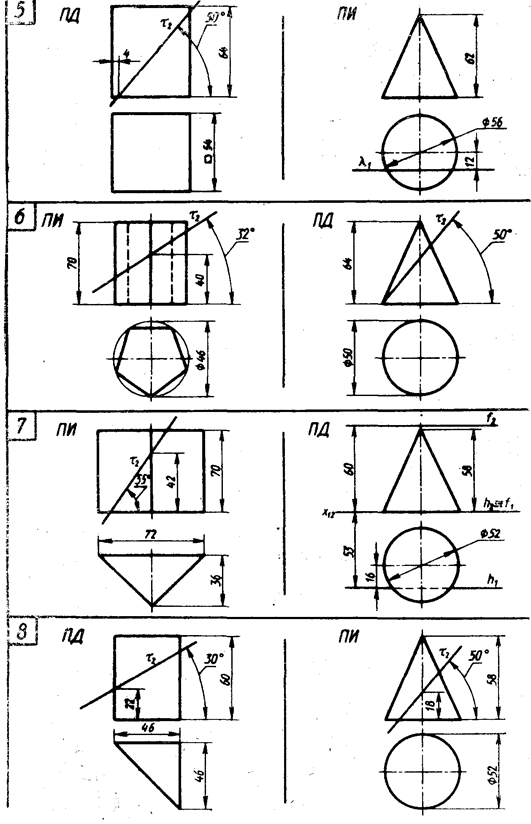
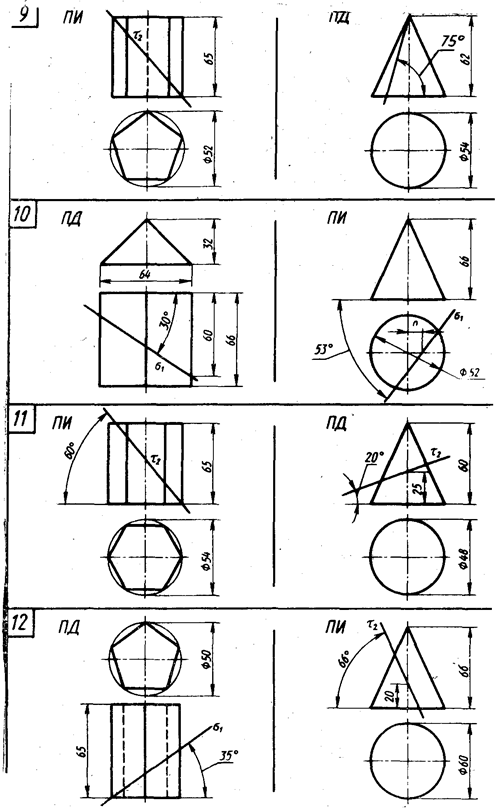
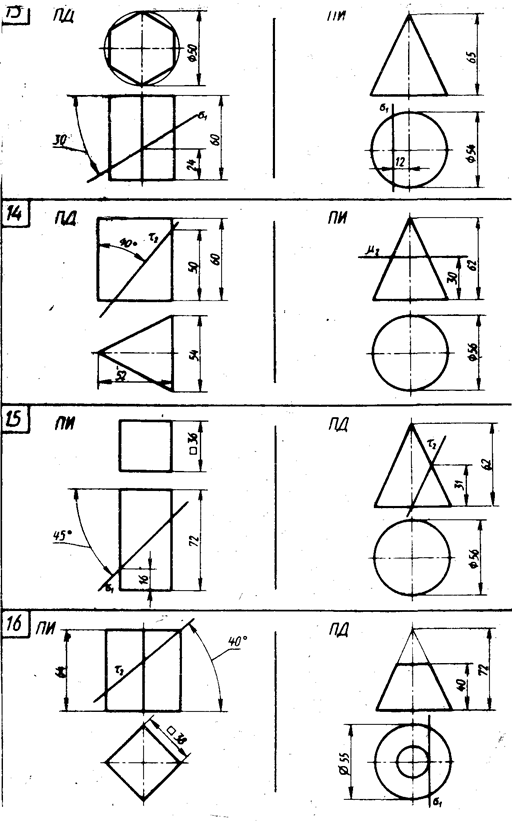
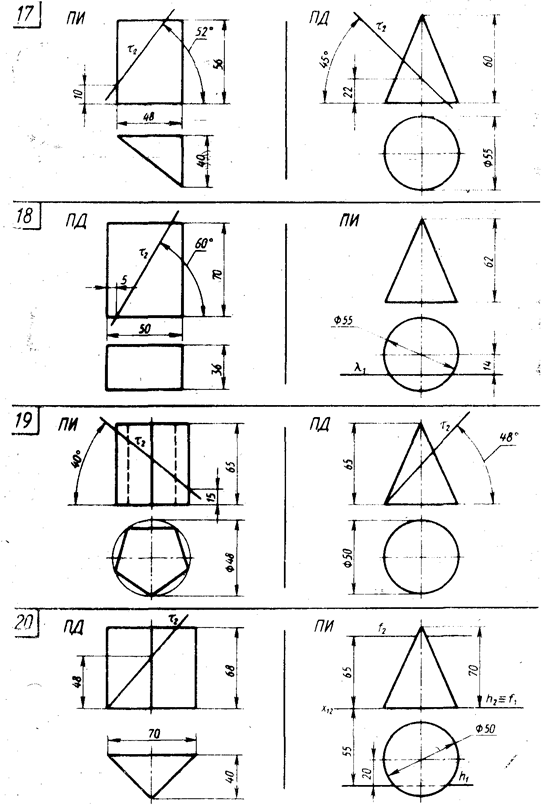
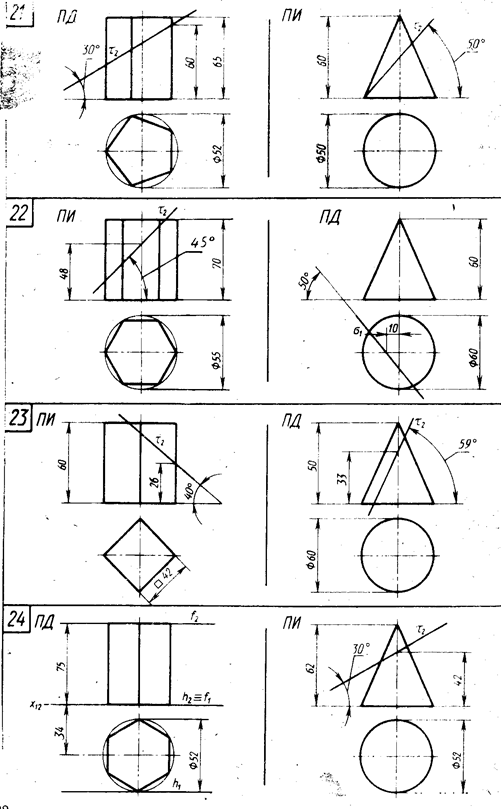
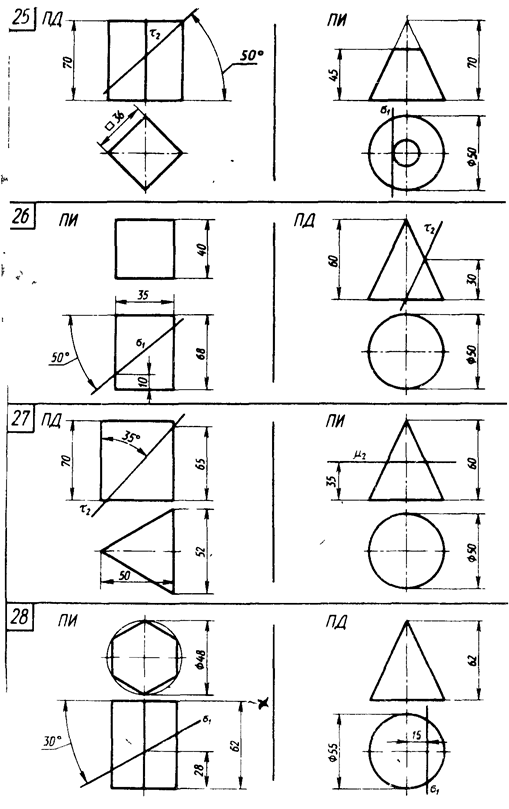
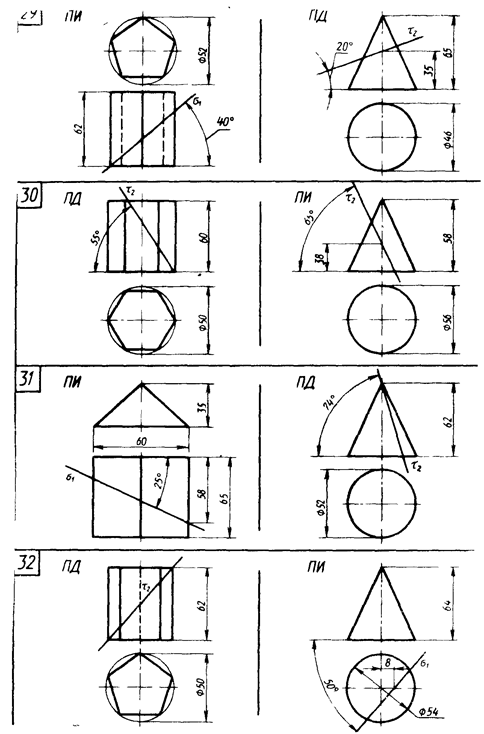
Рисунок 6 – Данные к задаче 4
Необходимо:
1. Выполнить чертеж выбранного геометрического тела.
2. Найти проекции фигуры сечения плоскостью Р.
3. Построить натуральную величину фигуры сечения, используя метод -вращения вокруг фронтального следа Pv плоскости Р или горизонтального следа РнПримеры выполнения задачи № 4 показаны на рисунках 7 и 8.
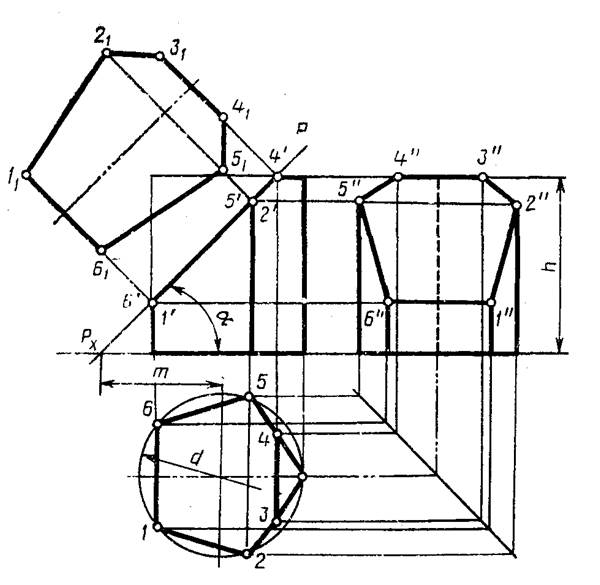
Рисунок 7 - Пример выполнения задачи № 4 (пересечение призмы)
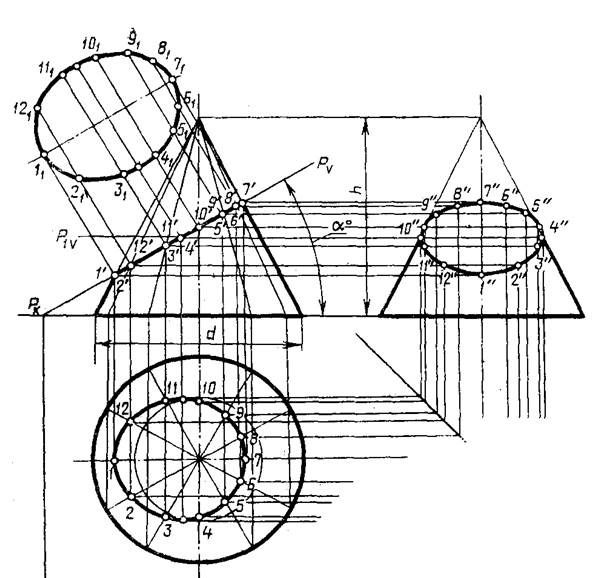
Рисунок 8 - Пример выполнения задачи № 4 (пересечение конуса)
Задача № 5. Тема: Взаимное пересечение поверхностей геометрических тел.
Для решения этих задач необходимо применять метод секущих плоскостей.
Даны: взаимно пересекающиеся поверхности геометрических тел.
Необходимо построить линии пересечения поверхностей геометрических тел.
Варианты указаны на рисунке 9 (стр. 27…34). Примеры выполнения задачи № 5 показаны на рисунках 10, 11.
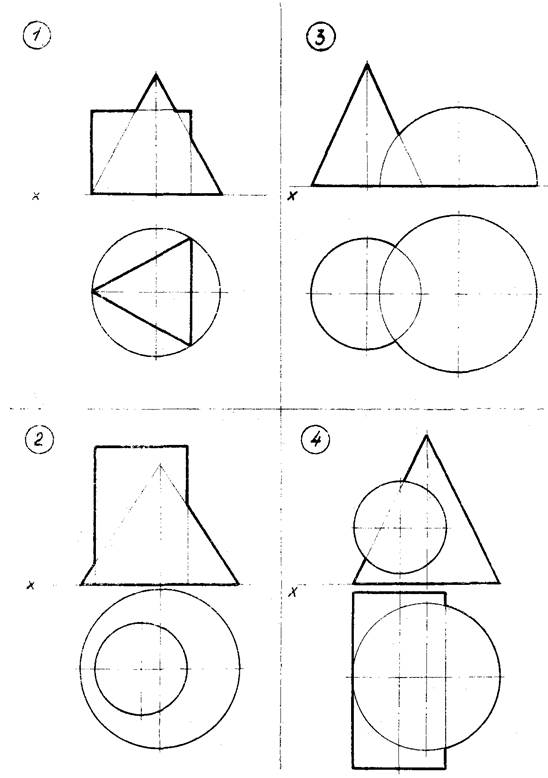
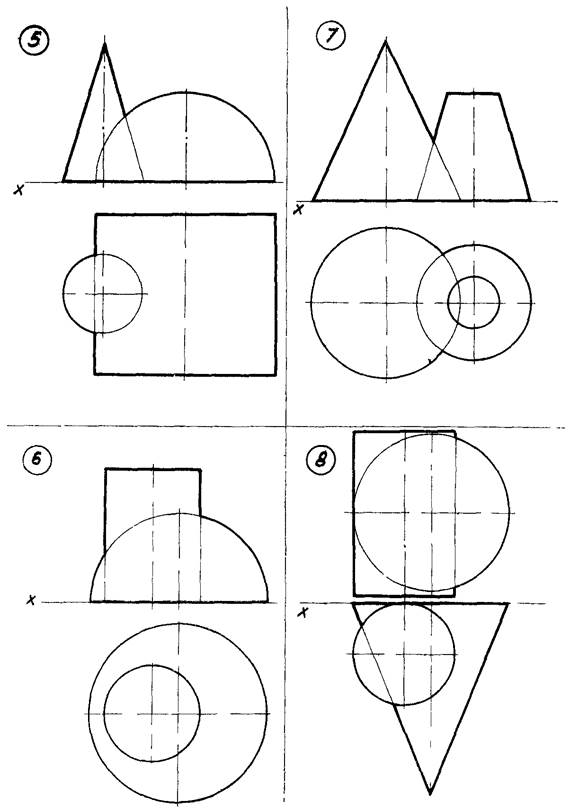
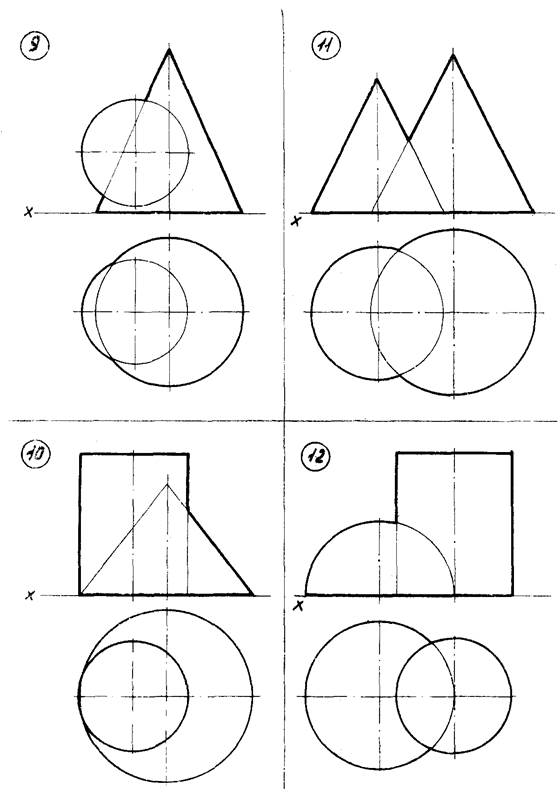
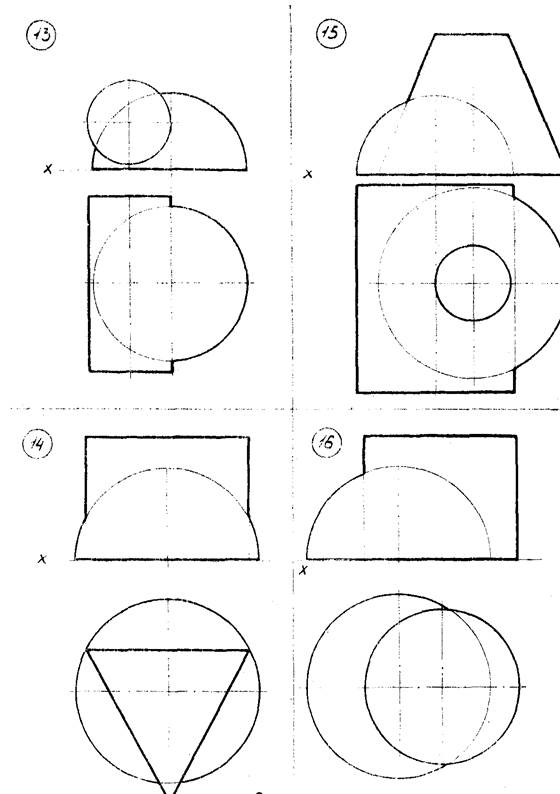
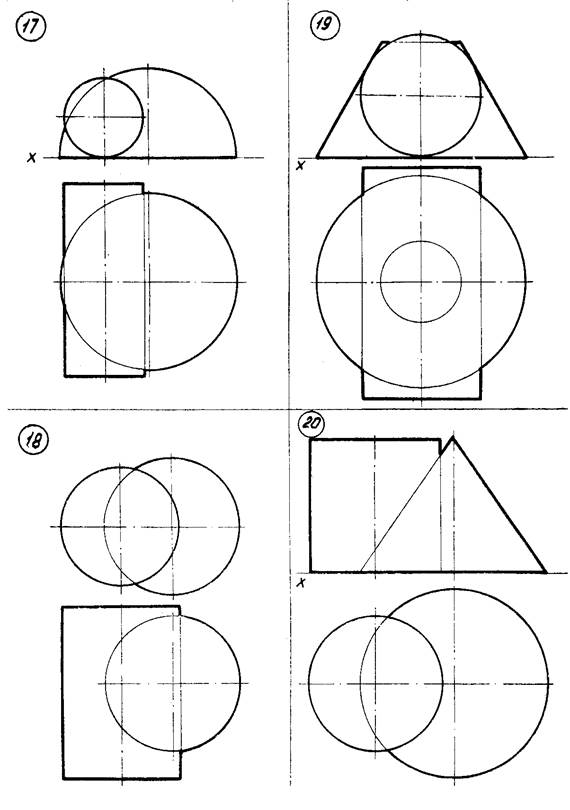
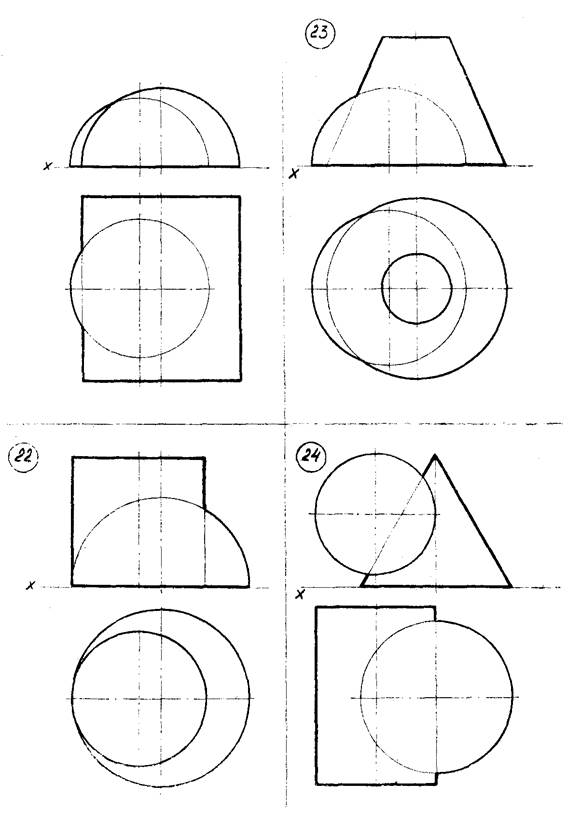
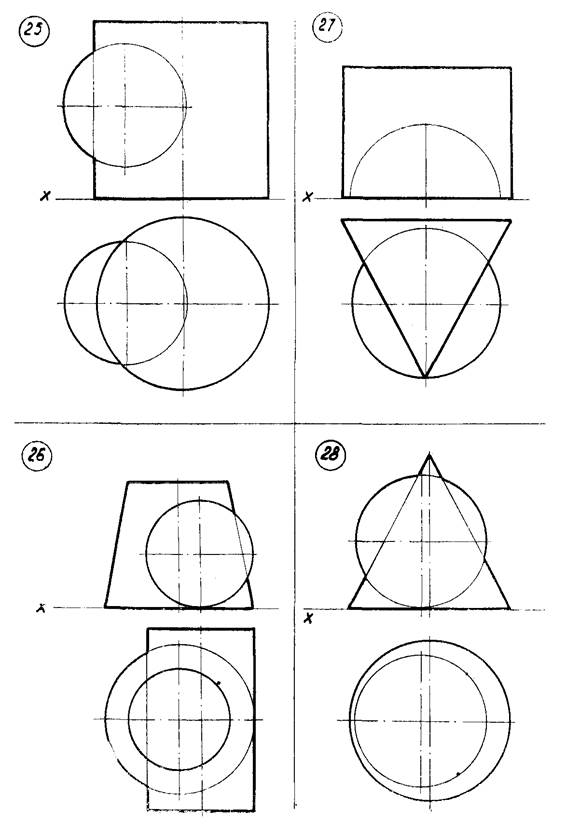
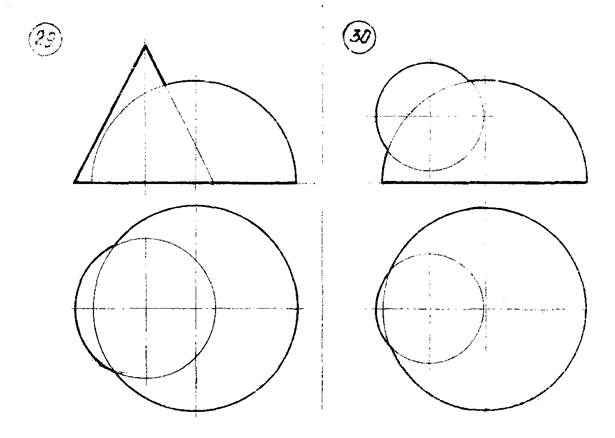
Рисунок 9 – Данные к задаче 5
Указания для выполнения задачи № 5
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.