Порядок изучения курса. Контрольная работа. План решения задач № 1-5, страница 4

Необходимо:

2.1.  Построить чертеж треугольника ABC

2.2.  Найти точку встречи прямой MN с треугольником ABC и определить, какая часть прямой видима на эпюре.

2.3.  Определить истинную величину прямой MN методом прямоугольного треугольника и углы ее наклона к плоскостям проекций Н и V.

Пример выполнения задачи № 2 показан на рисунке 4.

План решения задачи № 2. (Первая задача)

1.  Для нахождения точки встречи прямой с плоскостью прямую MN заключают во фронтально-проецирующую плоскость Р (эта плоскость перпендикулярна фронтальной плоскости проекций V). На рисунке 4 показан фронтальный след P_V (можно прямую MN заключать в горизонтально-проецирующую плоскость, плоскость перпендикулярную горизонтальной плоскости проекций Н).

2.  Плоскость Р рассекает плоскость ABC на линии 1'2'. Находим горизонтальную проекцию линии пересечения 12.

3.  Там, где горизонтальная проекция линии пересечения 12 отсекает прямую mn, там точка К встречи прямой MN с плоскостью ABC.

4.  По линии проекционной связи находимо фронтальную проекцию точки встречи К'.

5.  Определяем, какая часть прямой MN видима, а какая не видима. Видимость на фронтальной проекции (вид спереди) определяется по горизонтальной проекции (по виду сверху). По виду сверху определяем, какая точка n или m ближе к нам, т.е. какая координата Y больше. В нашем случае координата Y для точки n больше, чем для точки m. Поэтому на виде спереди прямая n'к' видима, а затем она проходит под плоскостью ABC и от точки 1´ до m' опять видима.

При виде спереди определяем, какая координата Zбольше, т.е. какая точка М или N удалена дальше от горизонтальной плоскости проекций Н. В нашем случае Z для m' больше, чем для n'. Поэтому при виде сверху мы сразу увидим отрезки mк, затем прямая проходит под плоскостью ABC и опять видима от bc до n.

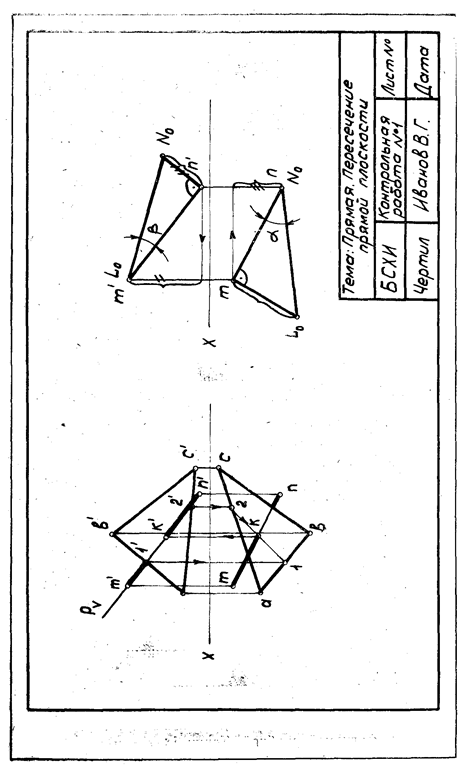Рисунок 4 - Пример выполнения задачи № 2

План решения задачи № 2 (вторая задача)

1. Для нахождения натуральной величины прямой на горизонтальной проекции (виде сверху) необходимо к mn под прямым углом пристроить катет mL₀, равный разнице удалений точек m' и n' от горизонтальной плоскости проекций. Эта разница (катет) показана на рисунке 4. двумя рисками и фигурной скобкой. Точку L_o соединяем с точкой n, там же находится и N_O. Получаем натуральную величину L_ON_O. А угол между L_oN_o и mn — это истинный угол а наклона прямой к плоскости Н.

2. Для нахождения натуральной величины прямой L_ON_O на фронтальной проекции (вид опереди) необходимо к rn'n' под прямым углом пристроить катет n'N₀ равный разнице удалений точек m и n от фронтальной плоскости проекций. Эта разница (катет) на рисунке 4. показана тремя рисками и фигурной скобкой. Полученную точку N_o соединяем с L_o. Таким образом, получаем натуральную величину прямой LoN_o. А угол между LoN_o и m'n' — это натуральный угол β наклона прямой L_ON_O к плоскости V.

Задача № 3. Темы: Пересечение плоскостей. Способы преобразования эпюра. *

Даны треугольники ABC и ДЕК в координатах X, У, Z. Данные взять в таблице 3.

Необходимо:

3.1.  Построить линию пересечения треугольников ABC и ДЕК и определить видимость на эпюре.

3.2.  Определить истинную величину треугольника ABC методом плоско-параллельного перемещения или другим методом.

Пример выполнения задачи № 3 показан на рисунке 5. План решения задачи № 3 (первая задача)

1.  Для нахождения линии пересечения треугольников необходимо найти точки пересечения (встречи с другим треугольником) любых двух прямых одного из треугольников. Для этого заключаем прямую DK во фронтально-проецирующую плоскость Р (плоскость Р перпендикулярную фронтальной плоскости проекций V) На эпюре фронтальный след P_v сливается с d'K'.