Основы научных исследований. Обработка экспериментальных данных и их анализ. Оформление отчета по УИРС, страница 7

Дополнительно в матрице планирования записываются три опыта на основном уровне для подсчета дисперсии.

Для сокращения числа опытов при большом числе факторов может быть использован дробный факторный эксперимент. В отличие от полного факторного эксперимента в этом случае не представляется возможным получить независимые (раздельные) оценки коэффициентов регрессии. Линейные эффекты смешаны с эффектами парных или тройных взаимодействий.

Матрица планирования дробного факторного эксперимента  (дробная реплика) для трех факторов  при  (полуреплика) приведена в табл.1.3.

Дробная реплика задается с помощью определяющего контраста. Для данного случая определяющий контраст

Система оценок коэффициентов регрессии при таком определяющем контрасте

 т.е.

 т.е.

 т.е.

Таблица 1.3

Матрица планирования (дробный факторный эксперимент), полу реплика

№ опыта						Условные обозначения строк
1	+	+	+	+		авс
2	+	-	+	-		в
3	+	+	-	-		а
4	+	-	-	+		с
5	-	0	0	0
6	-	0	0	0
7	-	0	0	0

6.  Установление вида математической модели.

На первом этапе математического планирования для отыскания направления к оптимуму достаточно построить линейную модель в виде уравнения регрессии

,                          (1.27)

где  - коэффициенты регрессии.

Для случая дробного факторного эксперимента линейная модель запишется в виде уравнения регрессии

7.  Расчет дисперсии и среднеквадратичной ошибки опыта.

Значения  и  рассчитываются по результатам опытов 5, 6, 7 (табл. 1.2) с использованием формул (4) и (5) приложения.

8.  Расчет коэффициентов регрессии и их доверительных интервалов.

Коэффициенты регрессии рассчитываются по формуле

,                                       (1.28)

где  - кодовые значения факторов в каждом опыте (берутся в соответствующем столбце матрицы планирования). При подсчете коэффициента  берутся значения  для каждого опыта. Доверительный интервал коэффициентов регрессии

,

где  - критерий Стьюдента для выбранного Р и числа опытов в матрице .

9.  Оценка статистической значимости коэффициентов регрессии.

Проверка значимости коэффициентов регрессии проводится:

а) сравнением абсолютной величины коэффициента с его доверительным интервалом .

Коэффициент считается статистически значимым при выполнении условия

или

б) сравнением расчетного и табличного  - критерия (коэффициентов Стьюдента)

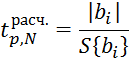
Коэффициент статистически значим при выполнении условия

Статистически незначимые коэффициенты из уравнения регрессии исключаются.

10.   Проверка адекватности математической модели (уравнение регрессии).

Проверку адекватности модели проводят по критерию Фишера (F- критерию)  или критерию Стьюдента (t - критерию), сравнивая расчетные и табличные их значения.

, где  - число степеней свободы, определяемое как разность между числом опытов и числом коэффициентов, включая ;

 - дисперсия неадекватности

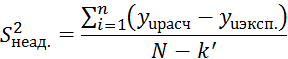
где  - значение параметра, оптимизации в u опыте, рассчитанное по уравнению регрессии;

 - значение параметра оптимизации, определенное экспериментально.

Уравнение адекватно, если

( берется из таблицы 2 приложения).

При оценке адекватности модели по t - критерию сравнивается расчетное и табличное его значения

.

Модель адекватна, если

( - берется из таблицы 1 приложения).

1.4.   Оформление отчета по УИРС.

Отчет должен содержать подробную информацию о существе проведенного исследования, давать исчерпывающую характеристику объекта исследования, включать подробный и тщательный анализ погрешности измерения и полученных результатов.