Для нахождения по методу наименьших квадратов искомой прямой поступают
следующим образом: проводят ординаты точек ![]() до их пересечения с
прямой. Значения этих ординат
до их пересечения с
прямой. Значения этих ординат ![]() , расстояние по
ординате от точки
, расстояние по
ординате от точки ![]() до прямой равно
до прямой равно ![]() .
.
Прямая будет наиболее близка к искомой при
наименьшей сумме квадратов всех расстояний ![]() . Минимум этой суммы
может быть определен при использовании дифференциального исчисления.
. Минимум этой суммы
может быть определен при использовании дифференциального исчисления.
Коэффициент в уравнении ![]() и
и ![]() определяют из
уравнений
определяют из
уравнений
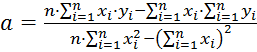 (1.21)
(1.21)
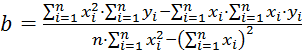 ,
(1.22)
,
(1.22)
где ![]() - число измерений.
- число измерений.
Суммирование производится по всем точкам.
Дисперсия коэффициентов ![]() и
и ![]()
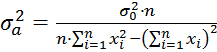 (1.23)
(1.23)
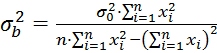 ,
(1.24)
,
(1.24)
где
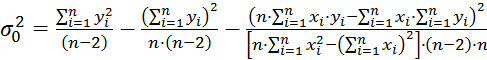 (1.25)
(1.25)
дисперсия отклонения точек от прямой.
1.3. Математическое планирование эксперимента для решения экстремальных задач.
Математическое планирование эксперимента ставит целью изыскание путей выполнения целенаправленного и эффективного эксперимента. Этот метод позволяет проанализировать процесс построением его математической модели и получить максимум информации при минимальных затратах.
Под экстремальными задачами понимают задачи, связанные с поисками экстремума (оптимума) в эксперименте.
Для решения экстремальных задач может быть использован метод крутого восхождения.
Этапы метода:
1. Постановка задачи, ее формулирование.
2. Выбор параметров оптимизации (Y).
Параметр должен быть однозначным, эффективным, характеризоваться численно, иметь ясный физический смысл. (Желательно, чтобы параметр оптимизации был единственным).
3. Выбор факторов ![]() . При этом выбираются
факторы, наиболее существенно влияющие на результат. После выбора факторов для
каждого из них выбирается основной уровень ( исходное значение) и интервал
варьирования.
. При этом выбираются
факторы, наиболее существенно влияющие на результат. После выбора факторов для
каждого из них выбирается основной уровень ( исходное значение) и интервал
варьирования.
Прибавление интервала варьирования к основному уровню дает верхний, а вычитание - нижний уровни фактора.
Факторы кодируют. Так, чтобы верхний уровень был +1, а нижний -1, при основном равном 0.
Кодовые значения факторов ![]() связаны с натуральными
связаны с натуральными
![]() соотношением
соотношением
![]() ,
(1.26)
,
(1.26)
где ![]() - натуральное значение
фактора на основном уровне;
- натуральное значение
фактора на основном уровне;
![]() - натуральное значение
интервала варьирования.
- натуральное значение
интервала варьирования.
При выборе интервала варьирования следует учитывать следующее:
а) интервал варьирования должен быть достаточно узким, т.к. чем уже интервал варьирования, тем больше вероятность возможности линейной аппроксимации.
б) интервал варьирования должен превышать ошибку его экспериментального определения (рекомендуется выбирать интервал варьирования, не превышающий удвоенной среднеквадратичной ошибки в определении данного фактора).
4. Составление таблицы условий эксперимента (табл. 1.1).
Таблица 1.1
Условия эксперимента
|
Факторы |
|
|
|
|
|
|
Основной
уровень |
|||||
|
Интервал
варьирования |
|||||
|
Верхний уровень (+1) |
|||||
|
Нижний уровень (-1) |
5. Составление матрицы планирования.
Количество опытов (N) определяется по формуле
![]()
где k - количество факторов оптимизации.
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, при этом называется полным факторным экспериментом.
Пример матрицы планирования при ![]()
![]() (табл. 1.2).
(табл. 1.2).
Таблица 1.2
Матрица планирования при ![]()
|
№ опыта |
|
|
|
|
Условные обозначения строк |
|
1 |
+1 |
+1 |
+1 |
ав |
|
|
2 |
+1 |
-1 |
+1 |
в |
|
|
3 |
+1 |
+1 |
-1 |
а |
|
|
4 |
+1 |
-1 |
-1 |
(1) |
|
|
5 |
- |
0 |
0 |
||
|
6 |
- |
0 |
0 |
||
|
7 |
- |
0 |
0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.