Основы научных исследований. Обработка экспериментальных данных и их анализ. Оформление отчета по УИРС, страница 4

Особое внимание следует обратить на техническое описание и паспортные данные приборов и оборудования, принцип работы, класс точности, пределы измерений, цену деления.

1.2.2.   Планирование эксперимента.

При планировании эксперимента необходимо:

- оценить объем эксперимента (число опытов), последовательность измерения факторов, выбор шага их изменения;

- спланировать эксперимент так, чтобы точность измерений соответствовала поставленной цели;

- учесть возможности появления систематических ошибок и принять меры к их устранению.

Ошибки измерений подразделяют на систематические, случайные и промахи. К систематическим относятся постоянные ошибки или ошибки изменяющиеся по определенному закону эти ошибки вызываются факторами, действующими одинаково при многократном повторении измерения и их можно подразделить на четыре группы:

1.  Ошибки, природа которых известна и величина которых может быть достаточно точно определена.

2.  Ошибки, природа которых известна, но величина которых не известна. К числу их относится ошибка измерительного прибора, которая определяется классом точности прибора (процент точности показания от всей действующей шкалы прибора).

Например, при замере силы тока с помощью миллиамперметра, класс точности которого 1,0, а шкала 75 мА, результат следует указывать с допуском  .

3.  Ошибки, о которых экспериментатор не подозревает, не смотря на значительную их величину.

Например, при определении плотности металла путем взвешивания численная величина плотности существенно зависит от наличия пузырей, раковин и т.д., которые должны учитываться при определении веса, объема.

4.  Ошибки, обусловленные свойствами (особенностями) измеряемого объекта.

Например, измерение диаметра цилиндра эллиптического сечения.

Эта ошибка может быть переведена в случайную. Систематические ошибки всегда можно устранить или учесть введением соответствующих поправок.

Случайные ошибки вызываются непостоянством условий эксперимента и не могут быть учтены.

Промахи это ошибки, значительно искажающие результат измерений и обнаруживаются уже в первых числах отсчета. Опыты, содержащие промахи, не учитываются.

1.2.3.   Обработка результатов измерений.

Для оценки величины случайной ошибки измерения существует несколько способов. Наиболее распространенным является способ оценки с помощью стандартной или средней квадратичной ошибки или средней арифметической ошибки.

Средняя квадратичная ошибка  определяется по формуле

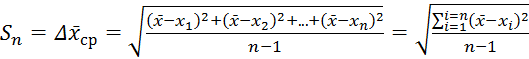,         (1.1)   где - среднее арифметическое значение измеряемой величины;

- число измерений.

Эта величина характеризует сходимость результатов отдельных измерений, т.е. степень их концентрации относительно среднего арифметического

.                                 (1.2)    

Будучи вычисленным на основе ограниченного числа опытов (3-5), среднее арифметическое является случайной величиной. Средняя арифметическая ошибка измерений

,                     (1.3)

Величина, равная , называется дисперсией измерений и является оценкой их точности.

Для оценки достоверности результатов измерений необходимо определить доверительный интервал при определенной доверительной вероятности (или коэффициент надежности).

Доверительный интервал - интервал значений измеряемой величины от  до , за пределы которого не должны выходить результаты преобладающего числа измерений при определенной доверительной вероятности Р. Доверительная вероятность - вероятность нахождения результатов отдельных измерений внутри доверительного интервала (вероятность того, что результаты измерения отличаются от истинного значения на величину, меньшую ). Доверительная вероятность (надежность) принимается равной при обычных измерениях 0,9 - 0,95 (или 90- 95 %), а для измерения с высокой степенью надежности - 0,99 (99 %).

При малом числе измерений определить дисперсию распределения  не представляется возможным.

В этом случае для определения доверительного интервала используется распределение Стьюдента.

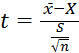 ,                                            (1.4) где  - коэффициент Стьюдента для числа измерений  и доверительной вероятности Р.

,                                       (1.5)