Основы научных исследований. Обработка экспериментальных данных и их анализ. Оформление отчета по УИРС, страница 5

Для нахождения доверительного интервала истинного значения величины  необходимо задаться требуемой доверительной вероятностью Р, определить по таблице 1 приложения значение коэффициента Стьюдента для имеющегося числа измерений  и по формуле (1.5) определить доверительный интервал.

Основные формулы используемые при обработке экспериментальных данных, приведены в приложении.

1.2.4.   Ошибка косвенных измерений.

Различают прямые и косвенные измерения. В случае прямых измерений интересующая нас величина определяется непосредственно, а в случае косвенных - непосредственно измеряется величина, от которой зависит нас интересующая.

Пусть интересующая нас величина  и измеряемая связаны уравнением

, где  и  - const.

Тогда всякому приращению  соответствует приращение

, где  - ошибка измерения;  - ошибка результата.

Если  при  малом по сравнению с измеряемой величиной          

,                                        (1.6)

Относительная ошибка

                                         (1.7)

При

                              (1.8)

                             (1.9)

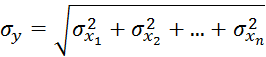                                    (1.10)

При

                            (1.11)

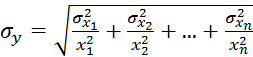                                    (1.12)

При

                                              (1.13)

                                             (1.14)

При

                                                 (1.15)

                                                 (1.16)

                                              (1.17)

Пользуясь дифференциальным исчислением ошибку функции  от переменных  при  можно представить в виде

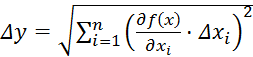,                               (1.18)

где  или - среднеквадратичные или среднеарифметические ошибки.

                                (1.19)

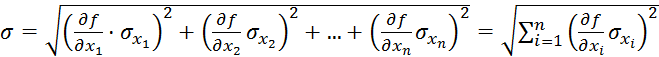,         (1.20)

1.2.5.   Оформление результатов измерений.

При записи результатов эксперимента необходимо указывать только значащие цифры и интервал возможных значений измеряемой величины. При этом под значащими следует понимать все цифры приближенного числа, начиная с первой слева, отличной от нуля и кончая последней верной цифрой (цифра, для которой погрешность не превышает единицы ее разряда).

Например .

Округлив результат до значащих цифр, имеем  или  .

Таким образом, количество значащих цифр в числе, указывающем измеряемую величину, является показателем ее точности.

Если целью эксперимента является установление функциональной зависимости между двумя величинами, целесообразно результаты эксперимента представить в виде графиков.

При построении графиков следует руководствоваться следующими рекомендациями:

1. До построения графика необходимо исследовать характер возможных изменений величин (наличие экстремумов, плавное изменение и т.д.).

2.  Масштаб по осям координат должен выбираться таким образом, чтобы можно было быстро определить координаты любой точки графика и учитывать погрешности величин, наносимых на график (самое малое деление на графике должно быть больше или равно абсолютной погрешности рассматриваемой величины).

3.  Целесообразно выбрать масштабную шкалу таким образом, чтобы график приближался к прямой линии. Например: при  ось абсцисс целесообразно выбрать логарифмической, т.к. в противном случае график будет параболой. При  целесообразна логарифмическая шкала и по оси абсцисс и по оси ординат.

4.  Нумерация делений на осях координат не обязательно должна начинаться с нуля, а с наименьшего значения аргумента или функции. В этом случае график располагается в центре рисунка.

5.  Результаты измерений должны наноситься на график с их погрешностями и линия графика должна проходить через участки прямоугольников. Количество точек по обе стороны от кривой должно быть примерно одинаково.

В случае, если необходимо установить функциональную зависимость между двумя величинами и определить коэффициенты в уравнении, выражающем эту зависимость, для проведения усредненной кривой целесообразно использовать метод наименьших квадратов.

Например: функциональная зависимость между величинами  и  выражается уравнением вида

.