

Отчет №8
Для ответа на вопрос: «Можно ли утверждать, что жители города, различающие своих оценках работы городских служб, различаются и по возрасту?» нужно использовать однофакторный дисперсионный анализ. Сделать его можно с помощью функции ANOVA. Для этого нужно создать переменную «возрастные группы», в моем случае все ответившие жители города Новосибирска разделены на 6 возрастных групп, так же используем раннее созданную переменную «оценка работы городских служб»
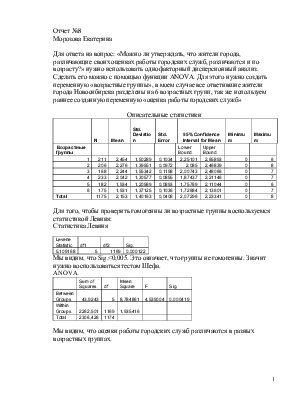
Описательные статистики
|
N |
Mean |
Std. Deviation |
Std. Error |
95% Confidence Interval for Mean |
Minimum |
Maximum |
|||||||
|
Возрастные Группы |
Lower Bound |
Upper Bound |
|||||||||||
|
1 |
211 |
2,454 |
1,50289 |
0,1034 |
2,25101 |
2,65893 |
0 |
6 |
|||||
|
2 |
206 |
2,276 |
1,39551 |
0,0972 |
2,085 |
2,46839 |
0 |
8 |
|||||
|
3 |
168 |
2,244 |
1,55342 |
0,1198 |
2,00743 |
2,48066 |
0 |
7 |
|||||
|
4 |
233 |
2,042 |
1,30577 |
0,0855 |
1,87437 |
2,21146 |
0 |
7 |
|||||
|
5 |
182 |
1,934 |
1,20589 |
0,0893 |
1,75769 |
2,11044 |
0 |
6 |
|||||
|
6 |
175 |
1,931 |
1,37125 |
0,1036 |
1,72684 |
2,13601 |
0 |
7 |
|||||
|
Total |
1175 |
2,153 |
1,40163 |
0,0408 |
2,07296 |
2,23341 |
0 |
8 |
|||||
Для того, чтобы проверить гомогенны ли возрастные группы воспользуемся статистикой Левиня:
Статистика Левиня
|
Levene Statistic |
df1 |
df2 |
Sig. |
|
5,109168 |
5 |
1169 |
0,000122 |
Мы видим, что Sig.<0,005. Это означает, что группы не гомогенны. Значит нужно воспользоваться тестом Шефа.
ANOVA
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
|
Between Groups |
43,9243 |
5 |
8,784861 |
4,539004 |
0,000419 |
|
Within Groups |
2262,501 |
1169 |
1,935416 |
||
|
Total |
2306,426 |
1174 |
Мы видим, что оценки работы городских служб различаются в разных возрастных группах.
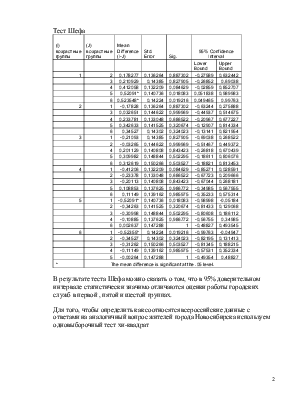
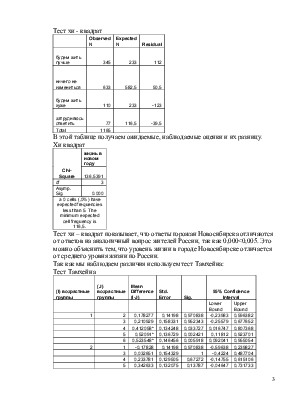
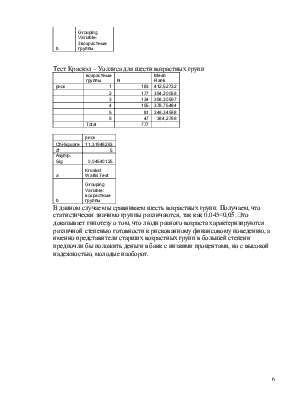
Тест Шефа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.