Влияет ли возрастной состав района на оценку будущего жителями районов. Доля людей, негативно оценивающих свое будущее

Страницы работы

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

Отчет9

Для того, чтобы проверить исследовательскую гипотезу: «влияет ли возрастной состав района на оценку будущего жителями районов» нужно построить модель простой линейной регрессии, где зависимый признак – доля людей, негативно оценивающих свое будущее, а независимый – доля людей старше 45 лет.

Первым шагом производим агрегирование исходного файла. Получаем две новые переменные с помощью функции Aggregate.

Следующим шагом рассчитываем коэффициент корреляции между зависимым и независимым признаками.

Коэффициент корреляции

		доля людей старше 45 лет	доля людей, негативно оценивающих свое будущее
доля людей старше 45 лет	Pearson Correlation	1	0,512054
	Sig. (2-tailed)		1,6E-79
	N	1175	1175
доля людей, негативно оценивающих свое будущее	Pearson Correlation	0,512054**	1
	Sig. (2-tailed)	0,000
	N	1175	1175
**	Correlation is significant at the 0.01 level (2-tailed).

В 99% доверительном интервале можно говорить о том, что целесообразно проводить дальнейший анализ, так как 0,000<0,05, то есть эти признаки зависят друг от друга.

Для построения модели линейной регрессии используем функцию Linear Regression.

Анализ полученных данных проводим в два этапа. Первый этап – анализ качества модели:

Model Summary(b)
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	0,512054	0,2622	0,261571	5,966052
a	Predictors: (Constant), доля людей старше 45 лет
b	Dependent Variable: доля людей, негативно оценивающих свое будущее

1. Коэффициент детерминации показывает долю дисперсии зависимого признака, объясненную независимым признаком. R Square=0,26, то есть 26% дисперсий признака «доля людей негативно, оценивающих свое будущее» можно объяснить признаком «доля людей старше 45 лет»

ANOVA(b)
Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	14837,66	1	14837,66	416,8612	0,00
	Residual	41751,5	1173	35,59377
	Total	56589,16	1174
a	Predictors: (Constant), доля людей старше 45 лет
b	Dependent Variable: доля людей, негативно оценивающих свое будущее

Coefficients(a)
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	-1,19326	2,191698		-0,54444	0,58624
	доля людей старше 45 лет	0,852247	0,041742	0,512054	20,41718	0,000
a	Dependent Variable: доля людей, негативно оценивающих свое будущее

2. Проверка равенства коэффициентов уравнения нулю.

Коэффициентом в пользуемся для проверки качества модели, так как в<0,05 принимаем альтернативную гипотезу о том, что от возраста зависит оценка будущего. Так же это говорит о прямой линейной зависимости между признаками, то есть если в районе увеличится доля людей старше 45 лет на 0,1, то доля людей негативно оценивающих свое будущее увеличится на 0,852.

В 50% случаев на долю людей, негативно оценивающих свое будущее, влияют люди в возрасте от 45 лет

3. Анализ остатков

Residuals Statistics(a)
	Minimum	Maximum	Mean	Std. Deviation	N
Predicted Value	38,86964	52,17979	43,41372	3,555074	1175
Residual	-9,47146	13,12819	0,000	5,96351	1175
Std. Predicted Value	-1,27819	2,465792	0,000	1	1175
Std. Residual	-1,58756	2,200481	0,000	0,999574	1175
a	Dependent Variable: доля людей, негативно оценивающих свое будущее

Переменная «остаток» должна быть нормально распределена. Нормальность распределения проверяем тестом Колмогорова-Смирнова

One-Sample Kolmogorov-Smirnov Test
		Unstandardized Residual
N		1175
Normal Parameters(a,b)	Mean	0,000
	Std. Deviation	5,96351
Most Extreme Differences	Absolute	0,190808
	Positive	0,190808
	Negative	-0,08933
Kolmogorov-Smirnov Z		6,54057
Asymp. Sig. (2-tailed)		0,000
a	Test distribution is Normal.
b	Calculated from data.

Так как 0,000<0,005 можно сделать вывод о том, что остатки нормально распределены. Можно сделать выводом о том, что получившееся модель достаточно качественная и можно перейти ко второму шагу – интерпритация полученных результатов:

Модель можно записать в виде формулы:

У=a+bx, где х-доля людей старше 45 лет (независимый признак), у- доля людей, негативно оценивающих свое будущее (зависимый признак).

У=-1,19+0,852*48,3=39,96

При увеличении доли людей старше 45 лет на 0,01(1 год) в Дзержинском районе, доля людей негативно оценивающих свое будущее увеличится на 0,852 и будет равна 39,96

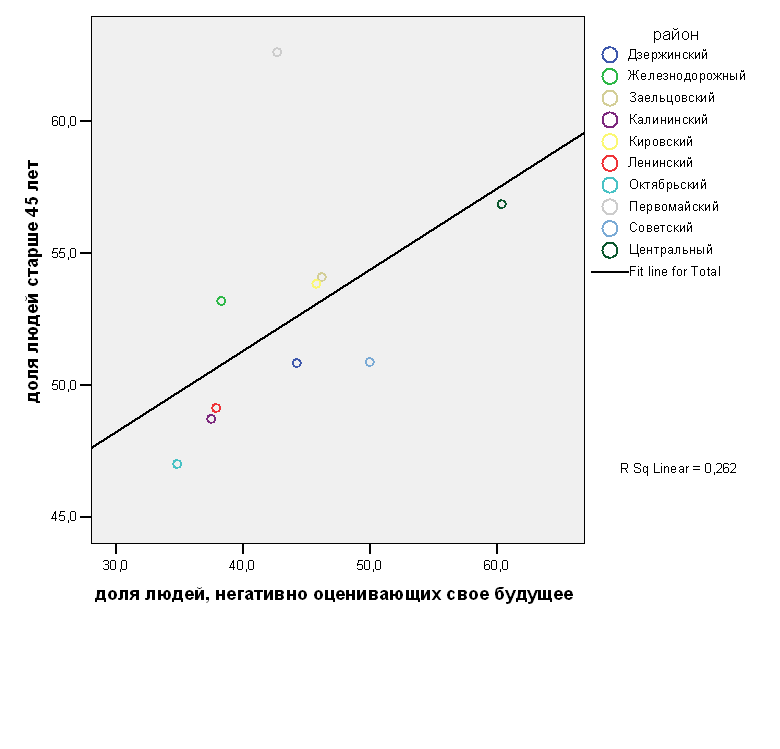
Эффект гетероскедастичности отсутствует, мы видим примерно одинаковое прилегание объектов к прямой. Все районы, за исключением Заельцовского района прилегают к прямой равномерно.