Химия \ Химия

Физическая химия в вопросах и ответах. Применение термодинамики к фазовым равновесиям. Верхняя и нижняя границы кривых испарения жидкости

Страницы работы

25 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

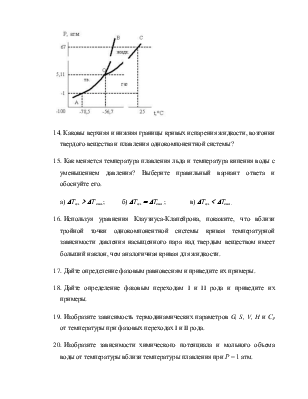
диаграммы состояния воды видно, что изобара при Р = 1 атм пересекает кривую плавления в точке, отвечающей температуре плавления льда, при которой существуют фазовое равновесие Н₂О_(лед) Û Н₂О_(ж)и Dm = 0, т.е. m_(лед) = m_(ж). 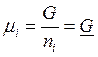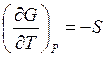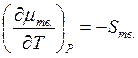Для индивидуального вещества химический потенциал представляет собой молярное значение энергии Гиббса , а , и зависимость химического потенциала от температуры для твердой и жидкой фаз выражается соответствующими уравнениями:

и 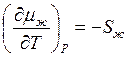. Поскольку величина энтропии всегда положительна, то химические потенциалы жидкой воды и льда вблизи температуры плавления убывают линейно, а наклоны прямых определяются величиной энтропии: S_лед<S_ж , поэтому 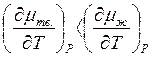, т.е. m_ж= f(T) идет круче.

Объем твердой и жидкой фаз с повышением температуры увеличивается, а при Т = Т_пл_. объем меняется скачком, причем V_льда>V_ж для воды (DV¹ 0).

21. Ответ

При температуре кипения между жидкой водой и паром устанавливается гетерогенное равновесие, относящееся к фазовым переходам I рода:

Н₂О_(ж) Û Н₂О_(пар), условием которого является равенство химических потенциалов: m_(ж)= m_(пар)или Dm_исп.= 0. При повышении температуры m_(ж) и m_(пар) уменьшается, т.к. 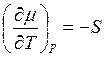, а S всегда положительна. Чем больше S, тем круче идет кривая m = f(T). Поскольку S_(пар)> S_(ж), то убывание функции m_(ж)= f(T) отразится на графике более пологой кривой, чем m_(пар)= f(T).

Энтропия жидкой воды меньше, чем энтропия пара S_(ж)<S_(пар) и при Т_кип_.энтропия меняется скачком: S_(пар)– S_(ж)= DS_(исп.).

22. Ответ

Уравнение зависимости Т_пл.= f(P) можно получить из уравнения Клаузиуса-Клапейрона для равновесия Т = Ж

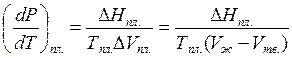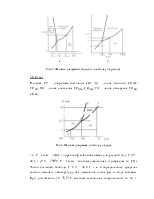
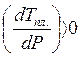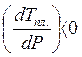, . Поскольку DН_пл_.> 0, то характер изменения Т_пл. с давлением зависит от знака DV: если V_ж> V_тв. для вещества А, то и с повышением давления Т_пл_. увеличится. Если же V_ж<V_тв_. для вещества В (как у воды), то DV< 0, и с повышением давления Т_пл_. понизится.

23. Ответ

Нет, эта форма уравнения является частным случаем уравнения Клаузиуса-Клапейрона: 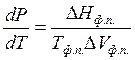. Оно может быть применено к процессам возгонки твердого вещества и испарения жидкости, когда DV»V_п (V_п>>V_тв.и V_п>>V_ж) и пар ведет себя как идеальный газ V_п= , тогда 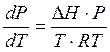или .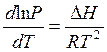

24. Ответ

При изменении температуры индивидуального вещества меняется его агрегатное состояние, т.е. происходят фазовые переходы. В изобарно-изотермическом процессе перехода вещества из состояния 1 в состояние 2 DG = G₂– G₁ £ 0, и, следовательно, процесс возможен, если G₂<G₁ , при этом вещество переходит из фазы 1 с бόльшим значением энергии Гиббса G₁ в фазу 2 с меньшим значением G₂. При Т = Т_ф.п. DG = 0, т.е. переход вещества из одной фазы в другую не сопровождается изменением энергии Гиббса и может происходить в обоих направлениях, при этом две фаза (два агрегатных состояния) находятся в равновесии. Для каждого агрегатного состояния G является функцией температуры: G_тв.(Т), G_ж(Т), G_г(Т), но по-разному изменяются с температурой, поскольку производная энергии Гиббса по температуре 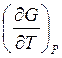= –S, а энтропия разных агрегатных состояний существенно различаются: S_тв<S_ж<S_г. В соответствии с этим убывание функции G_тв.(Т) на графике отразится более пологой кривой, чем функция G_ж(Т), а последней, в свою очередь, - более пологой кривой, чем G_г(Т). При определенных значениях температуры эти зависимости G(Т) пересекаются: при температуре отвечающей точке пересечения кривых G_тв.(Т) и G_ж(Т), DG = 0, в равновесии находятся твердая и жидкая фазы, и таким образом, эта точка является точкой плавления (Т_пл_.). В точке пересечения кривых G_ж(Т) и G_г(Т) при определенном давлении будут сосуществовать жидкая и газообразная фазы, и это будет точка кипения (Т_кип_.) при заданном давлении. При Т^'< Т_пл_. устойчивой является твердая фаза, т.к. G_тв.< G_ж, а при Т^''< Т_пл – жидкая фаза, т.к. G_ж.< G_тв_..

25. Ответ

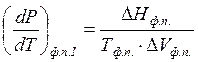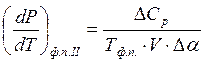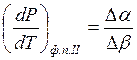Температура фазовых переходов, как первого, так и второго рода является функцией давления. Для фазовых переходов I рода (плавление, возгонка, испарение) эта зависимость описывается дифференциальным уравнением Клаузиуса – Клапейрона для равновесного существования фаз: . Для фазовых переходов II рода, где нет существования фаз, Р от Т_ф.п._II выражается одним из уравнений Эренфеста: и , где 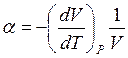- коэффициент термического расширения, 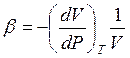– изотермический коэффициент сжимаемости. Как видно, зависимости Р = f (T_ф.п.) задаются с помощью тех термодинамических свойств, которые изменяются при переходе от одной фазы к другой. В случае фазовых переходов I рода это DН_ф.п. ≠ 0 и DV_ф.п. ≠0, а для фазовых переходов II рода это DС_р ≠ 0, Da≠ 0, Db≠ 0. Интересно, что последние величины – первые производные от тех, которые скачкообразно изменяются при фазовых переходах I рода.