Массовая кристаллизация из растворов. Равновесие между твердой и жидкой фазой. Кинетика процесса кристаллизации. Оценка кинетических параметров зародышеобразования и скорости роста кристаллов

Будем полагать в дальнейшем, что взаимодействия между кристаллами отсутствуют, а влияние фазы зародышей на перенос массы и энергии в смеси пренебрежимо мало.

С точки зрения механики сплошных сред каждая из выделенных нами фаз рассматривается как непрерывная. Тогда для каждой из фаз справедливы дифференциальные уравнения сохранения массы, импульса и энергии.

Запишем уравнения сохранения массы для фазы кристаллов объемом v и жидкой фазы:

для фазы кристаллов объемом  

,                                       (12.28)

для жидкой фазы

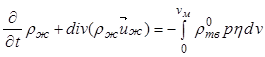.                       (12.29)

В ходе процесса кристаллизации уменьшение количества растворенной соли в растворе должно соответствовать количеству выделившихся кристаллов. Поэтому справедливо следующее уравнение сохранения массы соли в растворе:

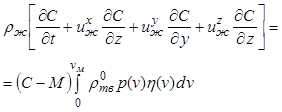.                   (12.30)

Здесь  - массовая концентрация соли в растворе;  - отношение молекулярных весов безводной соли, к кристаллогидрату (если полученное вещество безводное, то ); ,  - соответственно векторы скоростей жидкой фазы и фазы кристаллов объемом .

Для каждой из фаз гетерогенной смеси в ходе кристаллизации должен выполняться закон сохранения количества движения. Следовательно, можно записать соответствующие уравнения движения.

Уравнение движения для фазы кристаллов объемом  имеет вид

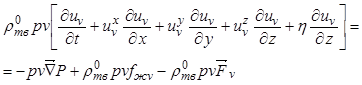,    (12.31)

где  - внешняя массовая сила, приходящаяся на фазу кристаллов объемом ;  - архимедова сила.

Сила взаимодействия между жидкой фазой и кристаллами в первом приближении определяется силой трения между фазами , которая для кристаллов размером  без учета стесненности составляет

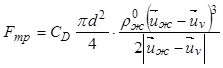.                                 (12.32)

Для жидкой фазы уравнение движения в условиях пренебрежимо малых вязких напряжений записывается в виде

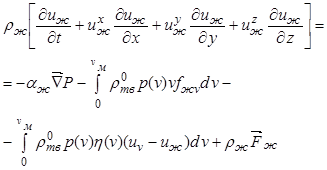.       (12.33)

Здесь член 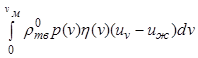 определяет изменение количества движения жидкой фазы за счет фазового перехода, а последний член  - влияние внешней массовой силы.

Запишем теперь уравнения сохранения энергии. Сначала выделим в качестве составляющей энергии многофазной смеси поверхностную энергию . Тогда внутренняя энергия смеси с учетом присутствующих фаз составит

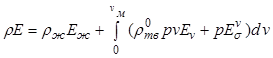,                     (12.34)

где  - поверхностная энергия сферической частицы объемом .

В дальнейшем при выводе уравнений энергии каждой фазы будем пренебрегать работой внутренних сил. В этом случае изменение внутренней энергии фазы будет определяться потоками теплоты, поступающими в фазу и покидающими ее. Для фазы кристаллов объемом  поток теплоты, поступающий к фазе, выражается формулой

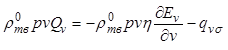,                                (12.35)

где первый член уравнения (11.164) определяет теплоту, получаемую фазой кристаллов объемом  при переходе кристаллов из одной фазы в другую вследствие их роста, а второй член соответствует потоку теплоты от фазы кристаллов объемом  к поверхности раздела фаз (не связанному с фазовым превращением). Так как внутренняя энергия  изменяется во времени и в пространстве с координатами (, , , ), то дифференциальное уравнение сохранения внутренней энергии для фазы кристаллов объемом запишется в виде

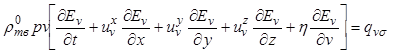.   (12.36)

Поток теплоты , поступающий к жидкой фазе, определяется потоком теплоты  от жидкой фазы к поверхности раздела фаз:

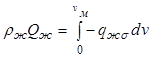.                                                   (12.37)

Тогда дифференциальное уравнение сохранения внутренней энергии для жидкой фазы примет вид

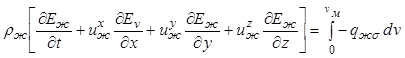.  (12.38)

Наконец, поток теплоты, , поступающий к поверхности раздела фазы кристаллов объемом , составляет

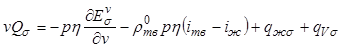,    (12.39)

где первый член уравнения отражает изменение поверхностной энергии кристаллов объемом  вследствие их роста, а второй - поток теплоты благодаря фазовому превращению (здесь ,  - соответственно энтальпия жидкой фазы и фазы кристаллов).

Соответствующее уравнение сохранения внутренней энергии для поверхности раздела кристаллов объемом  запишется в виде

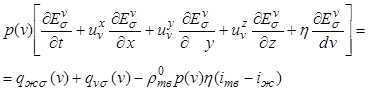.            (12.40)

Введем соответствующие температуры фаз , ,  и следующие уравнения состояния:

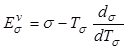,                                                         (12.41)

,                            (12.42)

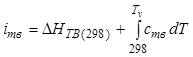,                                         (12.43)

где , ,  - температуры жидкой фазы, фазы кристаллов объемом  и поверхности раздела фаз соответственно;  - теплота растворения при концентрации насыщения: 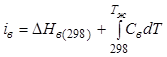; ; 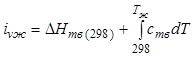,  - стандартные энтальпии воды и твердого вещества соответственно; ,  - удельные теплоемкости воды и кристаллизуемого вещества (предполагается, что кристаллизация происходит в водном растворе).

Входящие в систему уравнений математического описания процесса кристаллизации параметры  и  таковы:

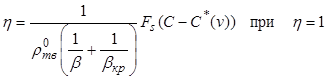,       (12.44)

.                                                             (12.45)

Коэффициент массоотдачи  можно определить из эмпирического соотношения