












Существенной частью математического описания реактора являются закономерности химических превращений.
Скоростью химической реакции называется количество вещества, которое реагирует или образуется в единицу времени в единице объема для гомогенных реакций и на единице внутренней поверхности катализатора для контактных реакций. Скорость реакции зависит от состава, температуры и давления реагирующей смеси, а для каталитических реакций - также от применяемого катализатора. Примем, что функциональные зависимости скорости от указанных переменных или кинетические уравнения известны.
Состав смеси может характеризоваться
массовыми концентрациями ![]() , объемными
концентрациями
, объемными
концентрациями ![]() , мольными долями
, мольными долями ![]() (которые для идеального газа
совпадают с объемными долями) и парциальными давлениями
(которые для идеального газа
совпадают с объемными долями) и парциальными давлениями ![]() ,
где
,
где ![]() - номер компонента.
- номер компонента.
Приведем формулы, связывающие эти переменные:
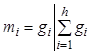 , (7.13а)
, (7.13а)
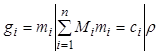 , (7.13б)
, (7.13б)
![]() , (7.13в)
, (7.13в)
![]() . (7.13г)
. (7.13г)
Здесь обозначены:
![]() -
молекулярный вес
-
молекулярный вес ![]() -гo
компонента;
-гo
компонента; ![]() - общее давление;
- общее давление; ![]() - температура,
- температура, ![]() ;
; ![]() -
универсальная газовая постоянная (если давление измеряется в барах, то
-
универсальная газовая постоянная (если давление измеряется в барах, то ![]() );
); ![]() -
плотность смеси;
-
плотность смеси; ![]() - число компонентов.
- число компонентов.
Формулы (7.13в) и (7.13г) справедливы,
если реакционную смесь можно считать идеальным газом. Там, где конкретный выбор
переменной, выражающей состав, несущественен, назовем ее концентрацией и обозначим
через ![]() .
.
Рассмотрим некоторые соотношения,
связанные со стехиометрией химических реакций. Пусть в системе, состоящей из ![]() компонентов, происходят
компонентов, происходят ![]() реакций. Количество
реакций. Количество ![]()
![]() -гo вещества в начальный и произвольный момент времени обозначим
соответственно через
-гo вещества в начальный и произвольный момент времени обозначим
соответственно через ![]() и
и ![]() , а количество
, а количество ![]() -гo вещества,
которое образовалось в результате
-гo вещества,
которое образовалось в результате ![]() -ой реакции -
через
-ой реакции -
через ![]() . Наконец, через
. Наконец, через ![]() обозначим стехиометрический
коэффициент
обозначим стехиометрический
коэффициент ![]() -гo вещества в
-гo вещества в
![]() -ой реакции, положительный для
продуктов реакций и отрицательный для реагентов.
-ой реакции, положительный для
продуктов реакций и отрицательный для реагентов.
Количества веществ, участвующих в реакции, относятся между собой как их стехиометрические коэффициенты, т.е.
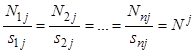 .
.
Общее значение этих отношений ![]() называют степенью завершенности
называют степенью завершенности ![]() -ой реакции.
-ой реакции.
Материальный баланс ![]() -гo компонента
запишем следующим образом:
-гo компонента
запишем следующим образом:
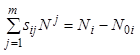 ,
,
![]() . (7.14)
. (7.14)
Без ограничения общности можно считать, что рассматриваемая система химических реакций линейно независима. Это значит, что векторы стехиометрических коэффициентов реакций, или столбцы стехиометрической матрицы
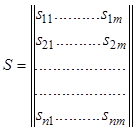 линейно независимы. Вследствие равенства
максимального числа линейно независимых строк и столбцов матрицы отсюда
следует, что, во-первых, строк (компонентов) не меньше, чем столбцов (реакций):
линейно независимы. Вследствие равенства
максимального числа линейно независимых строк и столбцов матрицы отсюда
следует, что, во-первых, строк (компонентов) не меньше, чем столбцов (реакций):
![]() , а во-вторых, найдется
, а во-вторых, найдется ![]() линейно независимых строк матрицы
линейно независимых строк матрицы ![]() . Примем, что это первые
. Примем, что это первые ![]() строк. Такого результата всегда
можно добиться, соответственно изменив нумерацию компонентов (т. е. строк
матрицы
строк. Такого результата всегда
можно добиться, соответственно изменив нумерацию компонентов (т. е. строк
матрицы ![]() ). Обозначим матрицу из первых
). Обозначим матрицу из первых ![]() строк через
строк через ![]() . Данная матрица - квадратная и
неособенная; это позволяет решить первые
. Данная матрица - квадратная и
неособенная; это позволяет решить первые ![]() уравнений
(7.14) относительно
уравнений
(7.14) относительно ![]()
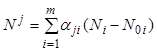 , (7.15)
, (7.15)
где ![]() -
элемент матрицы
-
элемент матрицы ![]() .
.
Подставив уравнение (7.15) в последние
(![]() ) уравнений (7.14), выразим
последние (
) уравнений (7.14), выразим
последние (![]() ) переменных
) переменных ![]() через первые
через первые ![]() переменных:
переменных:
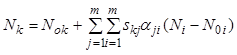 ,
, ![]() . (7.16)
. (7.16)
Общее число молей в системе выражается
через первые ![]() переменных
переменных ![]() по
формуле:
по
формуле:
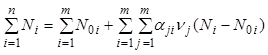 . (7.17)
. (7.17)
Здесь обозначено:
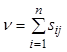 . (7.18)
. (7.18)
Введем в качестве переменной,
характеризующей состав смеси, удельное число молей ![]() -го
компонента, приходящихся на
-го
компонента, приходящихся на ![]() моль исходной
смеси
моль исходной
смеси ![]() :
:
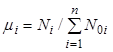 . (7.19)
. (7.19)
В начальный момент удельное число
молей совпадает с мольной долей: ![]() . Если реакции
идут без изменения общего числа молей, то это совпадение происходит в любой
момент. В общем случае мольная доля компонента выражается через удельное число
молей по соотношению:
. Если реакции
идут без изменения общего числа молей, то это совпадение происходит в любой
момент. В общем случае мольная доля компонента выражается через удельное число
молей по соотношению:
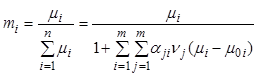 . (7.20)
. (7.20)
Последнее равенство выводится из уравнения (7.17).
Общая масса реагирующей смеси не меняется, поэтому из уравнения (7.16) следует аналогичное уравнение для массовых концентраций:
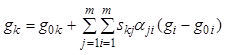 ,
, ![]() . (7.21а)
. (7.21а)
Разделив уравнение (7.16) почленно на 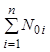 , получим аналогичное уравнение для
удельного числа молей:
, получим аналогичное уравнение для
удельного числа молей:
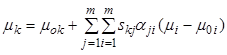 ,
, ![]() . (7.21б)
. (7.21б)
Если реакция протекает при постоянном объеме, то справедливо аналогичное уравнение для объемных концентраций:
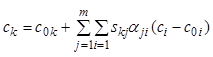 ,
, ![]() . (7.21в)
. (7.21в)
Уравнения (7.21) позволяют выразить
концентрации последних (![]() ) компонентов
через
) компонентов
через
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.