18.1. Преломление радиоволн
18.1.1. Общие определения
При определении траектории радиоволн в атмосфере используют метод приближения геометрической оптики. Лучевое представление справедливо для неоднородных сред с настолько медленным изменением коэффициента преломления, что на отрезке пути, соизмеримом с длиной волны в среде, можно принять пф) = const. При этом в первом приближении можно пренебречь отраженным лучом и свести процесс распространения к наличию только преломленного. Строгое решение уравнений Максвелла показывает, что такое приближение выполняется, если где = i/n(h) — длина волны в среде.
В атмосфере приближение геометрической оптики справедливо для всех волн радиодиапазона, за исключением диапазона ДВ (Х > 1000 м).
В гл. 17 показано, что диэлектрическая проницаемость атмосферы плавно меняется по высоте. Распространение радиоволн в такой среде сопровождается плавным искривлением траектории распространения — явлением рефракции.
При рефракции траектория представляет кривую, к которой касателен вектор, характеризующий скорость переноса энергии волны. Из курса технической электродинамики [18] известно, что при распространснии сигнала, энергия которого сконцентрирована в пределах полосы частот (00 — дотах) — (00 + дотах) И 00 » дотах, таким вектором в средс без дисперсии (тропосфера, стратосфера) является вектор фазовой скорости, а в среде с дисперсией (ионосфера) — вектор групповой скорости. В условиях атмосферы, где коэффициент преломления есть функция высоты, модули этих векторов равны [59]:
для фазовой скорости
![]() ф
ф![]() co/n(h), (18.1) где со скорость
распространения в свободном пространстве;
co/n(h), (18.1) где со скорость
распространения в свободном пространстве; ![]() n(h) = Ег (11) —
коэффициент преломления на высоте ,ђ•, для групповой скорости сигнала с
частотой 00 гр = СО + ] , (18.2)
n(h) = Ег (11) —
коэффициент преломления на высоте ,ђ•, для групповой скорости сигнала с
частотой 00 гр = СО + ] , (18.2)
где = (h,o) — коэффициент преломления в той области атмосферы, где наблюдается дисперсия.
Выражения показывают, что в атмосфере скорость
распространения волны различна на разных высотах. Поэтому элементы фронта ![]()
![]() волны,
распределенные в пространстве, перемещаются с разными ско
волны,
распределенные в пространстве, перемещаются с разными ско![]() ростями, что и является
причиной поворота фронта в процессе распространения, т.е. причиной рефракции.
ростями, что и является
причиной поворота фронта в процессе распространения, т.е. причиной рефракции.
Для нахождения траектории волны в приближении геометрической оптики неоднородную атмосферу разбивают на сферические элементарные слои столь малой толщины, что в пределах каждого слоя коэффициент преломления оказывается величиной постоянной, а траектория — прямолинейной. Только на границах слоев волна испытывает преломление, при этом скачок Ап при переходе от слоя к слою настолько незначителен, что интенсивность отраженной волны пренебрежимо мала по сравнению с преломленной.
Пусть на высоте h0 волна падает под углом (Ро на нижнюю границу преломляющей области, где коэффициент преломления изменяется скачком от по до (рис. 18.1). По
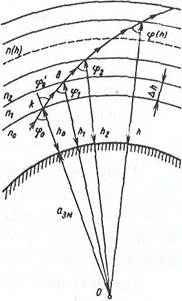
Рис. 18.1
закону преломления угол падения (Ро связан с углом преломления соотношением nosin(P0 ntsinoo. (18.3)
Поскольку в пределах элементарного слоя распространение волны происходит прямолинейно, то из треугольника okb (см. рис. 18.1) получаем
(аз», + sinqjl = (азу, + hl)/sinqfo, (18.4)
откуда связь между углами Фо, ф] на высотах [10, hl с учетом (18.3) определяется как
(азм
+ (Ц = (азм +![]() (18.5)
(18.5)
В результате преломления на границе элементарного слоя, расположенного на высоте h2, угол падения изменяется до значения (Ра, которое определяется из равенства
(аз», + /12)112 (h2)sinQ2 = (азх, + hl)nl ![]() —
—
![]() (18.6)
(18.6)
Согласно (18.5) и (18.6) для любой границы, расположенной
на высоте /1,![]()
(азм + h)n(h) sinq(h) = (азм + ho)no (ho)sintpo, (18.7)
![]() где величины, стоящие справа, относятся к
точке входа волны в преломляющую область.
где величины, стоящие справа, относятся к
точке входа волны в преломляющую область.
Из (18.7) угол падения волны в сферически слоистой атмосфере sin (РФ) = sinq)ono + + h)]. (18.8) Для плоскослоистой атмосферы (а зм 00) sin (P(h) = sin n(h). (18.9)
Полученные выражения показывают, что изменение наклона ![]() траектории
ф) зависит от перепада значений коэффициента преломления на пути следования
волны и чем более полога траектория, т.е. чем больше угол Фо, тем больше
отклоняется направление распростране
траектории
ф) зависит от перепада значений коэффициента преломления на пути следования
волны и чем более полога траектория, т.е. чем больше угол Фо, тем больше
отклоняется направление распростране![]() ния от первоначального.
ния от первоначального.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.