Распространение радиоволн в земной атмосфере. Преломление радиоволн. Общие определения. Траектория волны. Радиус кривизны траектории, страница 2

Другим параметром, характеризующим траекторию волны [кроме

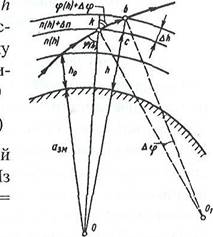
(P(h)], является радиус кривизны р. Для его определения выделим тонкий слой l\h, расположенный на высоте (рис. 18.2). На нижней границе слоя происходит искривление траектории, поскольку угол падения претерпевает скачок до. Радиус кривизны в точке перегиба при М 0

            р КЬ/Л(Р,                               (18.10)

где до — центральный угол, образованный нормалями к траектории в точках К и Ь. Из треугольника КЬс следует, что КЬ

— откуда

(18.11)

Рис. 18.2 определяется из закона преломления, записанного с учетом параметров атмосферы на высоте 11'. n(h)sinq)(h) = [n(h) + + до] =

(18.12) = [пф) + (P(h) cosA(P + cos (P(h) sin до].

Учитывая малость до, можно принять 1, sinlX(f) до, а произведение 0 как величину второго порядка малости.

Тогда из (18.12) имеем                      =                                 Подставляя это выражение в (18.11), получаем после перехода к пределу р = —n(h) /[dn / И sincp(h)]. (18.13)

Из (18.1 З) видно, что траектория отличается от прямолинейной (р 00) только при конечном значении градиента dn/dh, т.е. в неоднородных средах.

Знак минус в (18.13) означает, что величина р положительна и траектория обращена выпуклостью вверх, когда dn/dh < 0. При dn/dh > > 0 величина р отрицательна и траектория обращена выпуклостью вниз.

Необходимо также учитывать, что радиус кривизны траектории зависит от угла наклона траектории (P(h). При вертикальном падении, когда (РФ) = 0, (р 00), имеет место прямолинейное распространение.

18.1 З. Траектории радиоволн в тропосфере. Эквивалентный радиус Земли

Согласно данным гл. 17 у поверхности Земли относительная диэлектрическая проницаемость тропосферы отличается от единицы на несколько десятитысячных и в среднем убывает с высотой со скоростью, которая в стандартной тропосфере оценивается градиентом диэлектрической проницаемости 7,85 • 10-8 м-1 [см. (17.10)]. В такой слабо неоднородной среде траектории радиоволн испытывают малое искривление. Для оценки условий распространения наиболее сущсственным оказывается определение соизмеримости радиусов траектории распространения и Земли.

Радиус кривизны траектории в пределах тропосферы определяют по (18.13), принимая приземной значение = 0)

 (18.14) Для малых высот, где зависимость е (h) можно приближенно считать линейной и где dn /dh = = const [см. (119)], радиус кривизны рт(/1) = -2/[gT sinw(h)].       (18.15)

Для волн, распространяющихся по пологим траекториям вдоль Земли, когда —> 90⁰ и (РФ) —» 90⁰ , получаем выражение для радиуса кривизны рт =-2/gc.    (18.16)

Из (18.16) видно, что если на всем пути распространения градиент диэлектрической проницаемости есть величина постоянная, то траектория волны представляет собой дугу окружности, радиус которой определяется величиной градиента. В условиях стандартной тропосферы (17.10) РТст - 25 000 км.

При расчетах неудобно иметь дело с криволинейными траекториями. Этого можно избежать для области высот, где gT = const, вводя понятие эквивалентного радиуса Земли. В концепции эквивалентного радиуса принимается, что распространение происходит по прямолинейной траектории, но над Землей не с истинным радиусом азм, а с некоторым эквивалентным радиусом азм э (рис. 18.3). Величина азм э определяется из условия, что разность между значениями кривизны реальной траектории радиусом р и реальной Земли радиусом аз м равна разности между значениями кривизны спрямленной тра-