Входное сопротивление и сопротивление излучения. Теория длинных линий. Метод наведенных ЭДС и метод эквивалентной схемы

2.3. Входное сопротивление и сопротивление излучения

Приближенный расчет входного сопротивления СЭВ может быть осуществлен с использованием двух методов, описанных в 1.3: методом наведенных ЭДС [см. формулу (1.56)] и методом эквивалентной схемы. В настоящем разделе используется второй метод, основанный на аналогии тонких симметричных вибраторов с разомкнутой линией с потерями.

Из теории длинных линий [37] следует, что входное сопротивление линии с потерями, эквивалентной вибратору, Z =Zcthyl,  (2.13)

где 7, — комплексное волновое сопротивление линии (комплексность вызвана потерями в линии); у = (х + — комплексная постоянная распространения, — коэффициент затухания в линии, р — коэффициент фазы; I — длина эквивалентной линии, равная длине плеча вибратора. Остановимся на вопросе определения величин Z , а и [3.

Комплекснос волновое сопротивление длинной линии с потерями [37]

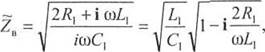                                              (2.14)

где R — погонное сопротивление каждого проводника длинной линии; Ц и С, — погонные индуктивность и емкость длинной линии; Z — волновое сопротивление линии без учета потерь в ней, причем 7. —  Поскольку с, где с — скорость света, имеем 7, = ТКС,. Величину С, определяют обычно методом Хоу, находя полную емкость вибратора как уединенного цилиндрического тела радиусом а и затем усредняя ее делением на общую длину вибратора L У. В результате для 4 получаем формулу

                                                                     (2.15)

Постоянная рапространения связана с погонными параметрами

L,C, и соотношением [37]

              (24 +ioLl)ioq.                                          (2.16)

При сравнительно малых значениях « (ВЦ), как следусг из анализа выражения (2.16), получается, что а = R,/Z , р = = К. При этом в (2.14) второй корень преобразуется к виду (1 — =

= — ia/(3). Окончательно получаем

          сх                                                    (2.17)

Коэффициент затухания (У, рассчитывается, как отмечалось в S 1 .З, из условия равенства мощности тепловых потерь в эквивалентной линии: l j(z) —Rldz. (2.18) 2 где коэффициент 2 перед интегралом учитывает наличие двух проводников в эквивалентной линии, мощности излучения симметричнотю электрического вибратора РЕ. Мощность РЕ определяется интегрированием среднего (во времени) значения вектора Пойнтинга (1. З 1) по сферической поверхности радиусом R в дальней зоне:

                     —ј R ² sinOdOdcp.                                                              (2.19)

24 о о

Вводя понятие сопротивления излучения RE как коэффициента пропорциональности между РЕ и половиной квадрата тока в пучности, т.е. = 2РЏ    , с помощью (2.19) и (2.7), получаем

7.? ^л[cos(klcos0) — cosk/] ² (2.20) sine

График зависимости RЕ от отношения l/i, полученный методом численного интегрирования, приведен на рис. 2.7. Отметим, что величина Щ, определяемая формулой (2.20), основанной на синусоидальном распределении тока, справедливом в первом приближении для тонких вибраторов, не зависит от толщины плеч вибратора и их формы. Приравнивая (2.20) и (2.18) и проводя интегрирование в последнем, окончательно получаем

sin 2kl

a=RE/120l ln—           (2.21) 2kl

Что касается коэффициента фазы [З, то оказывается, что в действительности этот коэффициент отличается от величины, равной К. Объясняется это учетом потерь, влиянием торцевой емкости между плечами вибратора, а также тем фактом, что Ц С, и R , для СЭВ, в отли-

чие от обычной длинной линии, переменны по длине вибратора. Обычно значения [3 берут из результатов эксперимента [2], которые свидетельствуют о том, что [З К, т.е. длина волны в эквивалентной линии Л = 27t/[3 меньше длины волны в свободном пространстве = 2л/К. Для повышения точности расчета по формуле (2.21) в ней также следует осуществить замену величины К на (3.

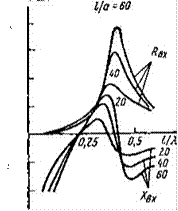
На рис. 2.8 приведены графики активной (Щ) и реактивной (Хвх) составляющих входного сопроптњления СЭВ, рассчитанного по формуле (2.13) для различных значе-

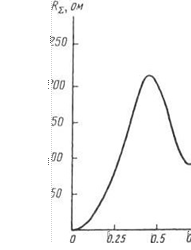
Рис. 2 7

Rn3n. Ой         ний радиуса вибратора а. Эти кривые, построенные в зависимости от соотношения П, можно при фиксированной частоте рассматривать как зависимости от длины плеча При фиксированном значении I эти же кривые харакгеризушг часгогные свойства вибраторов по входному сопротивлению. Анализ графиков позволяет сделать следующие выводы:

1.  Вблизи             0,25 и   0,5 реактивная составляющая Хн обращается в нуль,

при этом в окрестности l/i — 0,25 вибратор Рис, 2,8. велет себя подобно последовательному колебатсльному контуру, в окрестности = 0,5 — подобно параллельному контуру. Точное значение резонансных шин несколько меньше, чем 0,25i и что объясняется отмеченным выше отличием коэффициента фазы (3 от К. Таким образом, для точной настройки СЭВ в резонанс длину вибратора следуст несколько укоротить по сравнению с 0,251 (при посдедовательном резонансе) или 0,51 (при параллельном резонансе); всличина укорочения зависит от радиуса вибратора. При последовательном резонансе (!/i = 0,25) величина Щ, равна 73,1 Ом (для вибраторов с радиусом а —» О); при увеличении радиуса до 7 10-31 R = 94,8 Ом. При параллельном резонансе (ИЛ = 0,5) величина R сильно зависит от радиуса и составляет сотни и даже тысячи Ом (для вибраторов с а -9 О).

2.  Чем больше радиус вибратора, тем плавнсе кривые зависимострП их от частоты. Используя терминологию теории цепей, говорят, что толстые вибрагоры (вибраторы с низким волновым сопротивлснием) обладают меньшей добротностью по сравпсниео с тонкими вибртгорами. Такие нибртторы могут без перестройки работать в 00лес широкой полосе рабочих частот.