Оценка кинематических свойств при помощи коэффициента сервиса позволяет выбрать рациональный вариант структурной схемы исполнительного механизма. Эта задача сводится к выбору длин звеньев исполнительного механизма, вида и расположения кинематических пар, при которых значения θ достигают максимума.
Объединенный критерий манипулятивности и достижимости
Различие критериев геометрического синтеза обуславливает многокритериальность задачи. Известно, что в общем случае многокритериальные задачи неразрешимы по всем критериям одновременно: улучшение одних показателей влечет за собой ухудшение других. Выход из положения находится на пути создания искусственного критерия, в той или иной форме учитывающего все критерии.
Например, рекомендуется использовать комплексный критерий свертки манипулятивности и достижимости:
J=
V×
=
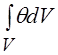
где q - коэффициент сервиса.
Интересно отметить, что рука человека устроена так, что именно этот критерий достигает в сагиттальной плоскости человека максимального значения (сагиттальная плоскость – плоскость симметрии человека).
Природа синтезировала следующие "оптимальные" соотношения звеньев руки:
l1/L=0,44¸0,47; l3/L»0,14; l1+l2+l3=L, где l1 – длина предплечья, l2 – длина плеча, l3 – длина кисти, L – общая длина руки.
Ограничения по существу являются условиями реализуемости операций, предписанных промышленному роботу техпроцессом.
1. Точки позиционирования должны быть достижимы, в манипулятивных точках должна реализовываться определенная ориентация схвата.
Проверка условий позиционирования и ориентирования состоит в решении обратной задачи кинематики:
=f (
)
или
=f(,
)
– вектор кинематических параметров МС;
– вектор
положения объекта манипулирования;
– вектор
ориентации схвата.
Если
решение такой задачи существует для точки ,
то ограничения выполняются.
2. При геометрическом синтезе возможны постановки, когда задаются ограничения на размеры последнего звена - схвата. Это связано с тем, что функциональное назначение схвата требует для его реализации определенных конструкторских решений, от чего сильно зависят размеры. Если не ограничивать снизу геометрические размеры последнего звена при геометрическом синтезе, то возможна ситуация, когда "спроектированные" размеры последнего звена не позволят конструктивно обеспечить функциональное назначение захватного устройства.
3. Возможно ограничение на максимальные размеры рабочей зоны - диаметр РЗ.
1. Задать кинематическую структуру МС.
2. Задать множество точек позиционирования и ориентирования.
3. Назначить значения геометрических параметров МС.
4. Решением обратной задачи кинематики проверить ограничения.
5. Оценить качество МС на основе выбранного критерия.
6. Если качество неудовлетворительное (не найден extr), выбрать новое приближение на основе определенного алгоритма принятия решения и перейти к п.3. В противном случае задача решена.
7. Найти ограничения на обобщенные координаты, как max и min их значения по всем технологическим точкам.
Пример задачи геометрического синтеза
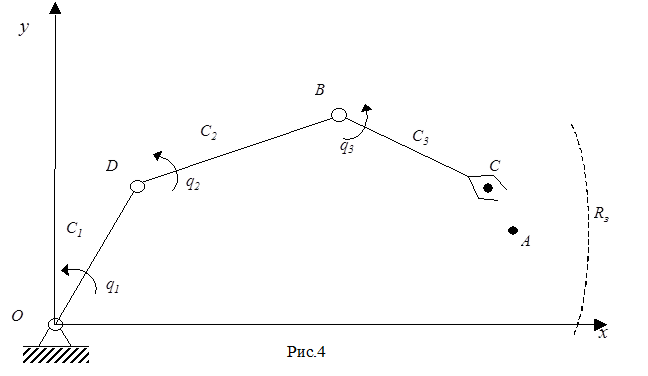
Задана структура трехстепенной плоской МС (рис. 4).
Длина третьего звена (схвата) С3 задана. Радиус рабочей зоны не должен превышать наперед заданной величины Rз:
C1+C2+C3£Rз
Требуется выбрать размеры С1, С2 МС так, чтобы коэффициент сервиса в точке А принимал максимальное значение:
q=f(q1A,q2A,q3A,C1,C2)®max
Для решения задачи можно предложить следующий алгоритм.
1. Следует задать радиус Rз рабочей зоны, координаты точки позиционирования А(xA,уA), размер С3 последнего звена (схвата).
2. Поиск оптимальных значений параметров С1, С2 осуществляется назначением конкретных значений этих параметров.
3. При C1+C2+C3>Rз нарушается ограничение на размеры РЗ. В этом случае следует перейти к п.2, иначе - к следующему пункту.
4. Как следует из рис.2, координаты центра схвата связаны с обобщенными координатами q1,q2,q3 зависимостями:
xc=C1 cos q1+C2cos(q1+q2)+C3cos(q1+q2+q3)
yc=C1 sin q1+C2sin(q1+q2)+C3sin(q1+q2+q3).
Если окажется, что при любых q1,q2,q3
xc2+yc2<xA2+yA2, что равносильно условию
C1+C2+C3<
OA, то точка А
для МС недостижима и следует обратиться к п.2.
5. Точка А достижима. Вычисляем значение коэффициента сервиса в ее окрестности. Для этого меняем угол j3 (рис.5) в пределах j3Î[-p,p] c определенным шагом Dj.
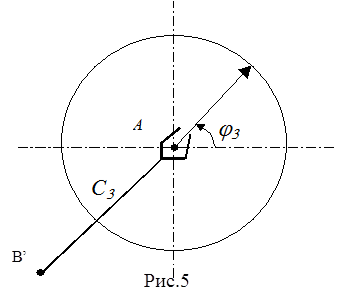
При этом точка B’(xB’, yB’) будет иметь координаты:
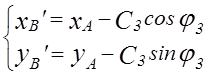
Если точка В’ достижима для двухзвенника ОDВ, то соответствующая ориентация схвата (и ее окрестность ± Dj /2) включается в угол сервиса.
Варьирование j3 позволяет таким образом оценить значения угла сервиса jA в точке А и, следовательно, коэффициент сервиса
q=jA/2p.
Если точка В’ недостижима, то можно считать окрестность соответствующего угла j3 исключенной из угла сервиса.
Аналитически условие достижимости точки В’ эквивалентно выполнению неравенства
xB2+yB2³xB’2+yB’2
или
C1+C2³
.
6. Если вычисленное значение qA максимально либо достаточно близко
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
