Кинематический расчет привода. Подбор электродвигателя. Уточнение передаточных чисел привода. Определение частот вращения и вращающих моментов на валах привода, страница 4

Коэффициент нагрузки K_F при расчете по напряжениям изгиба [1]:

К_H = К_Fv∙K_Fb∙K_Fa,                                                (13)

где К_Fv – коэффициент, учитывающий внутреннюю динамику нагружения, связанную с ошибками шагов зацепления шестерни и колеса; K_Fb – коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца; K_Fa – коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями.

Значения коэффициента К_Fv, учитывающего внутреннюю динамику нагружения принимают по табл. 2.9 [1]:

-  К_Fv = 1,04.

Коэффициент K_Fb, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца вычисляют по формуле [1]:

K_Fb = 0,18+0,82∙K_Hb⁰.

Подставим известные значения коэффициентов:

K_Fb = 0,18+0,82∙K_Hb⁰ = 0,18 + 0,82∙1,0104 = 1,0085.

Коэффициент K_Fa, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями определяют так же, как при расчетах на контактную прочность: K_Fa = K_Ha⁰:

-  K_Fa = K_Ha⁰ = 1,24.

Подставим все найденные значения коэффициентов в выражение (13):

К_H = К_Fv∙K_Fb∙K_Fa = 1,04∙1,0085∙1,24 = 1,3006.

Подставим все значения коэффициентов и величин в выражение (12):

.

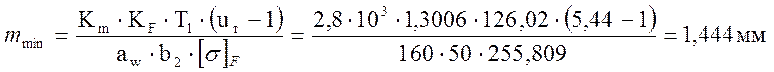Из полученного диапазона (m_min…m_max) принимают наименьшее значение, согласуя его со стандартным:

-  m = 1,5 мм.

Число зубьев колес и угол наклона. Фактическое передаточное число

Минимальный угол наклона зубьев косозубых колес b_min быстроходной ступени [1]:

b_min = arcsin (4∙m/b₂) = arcsin (4∙1,5/50) = 6,9°

Суммарное число зубьев z_s [1]:

-  z_s = 2∙a_w∙Cosbmin/m = 2∙160∙Cos6,9°/1,5 = 211.

Действительное значение угла b наклона зуба быстроходной ступени:

b_б = arccos [(z_s∙m/2∙a_w)] = arccos [(211∙1,5/2∙160)] = 8,482°.

Число зубьев шестерни z₁ и колеса z₂ [1]:

-  z₁ = z_s/(u_т – 1) = 211/(5,44 + 1) = 33;

z₂ = z_s - z₁ = 211 - 33 = 178.

Фактическое передаточное число u_ф [1]:

-  u_ф = z₂/ z₁ = 178/3 = 5,39.

                                                    Диаметры колес

Делительные диаметры d, мм [1]:

шестерня: d₁ = z₁∙m/Cosb = 33∙2.5/Cos8.482=50.05мм;

     колесо: d₂ = 2∙a_w + d₁ = 2∙160 -50.05  =265.395  мм.

Диаметры d_а и d_f окружностей вершин и впадин зубьев [1]:

      d_а1 = d₁ + 2∙m = 50.05 + 2∙1.5 = 53.05 мм;

      d_f1 = d₁ – 2∙1,25∙m =50,05 – 2∙1,25∙1.5 = 46,3 мм;

      d_а2 = d₂ + 2∙m = 265,95+2∙1,5 = 268,95 мм;

      d_f2 = d₂ - 2∙1,25∙m = 265,95 - 2∙1,25∙1,5 = 262,2 мм.

Проверочный расчет зубьев по контактным напряжениям

Расчетное значение контактного напряжения s_Н [1]:

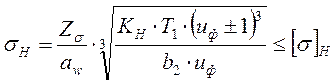,                                   (14)

где Z_s = 9600 для прямозубых передач и Z_s = 8400 для косозубых передач, МПа^1/2.

Подставим все значения коэффициентов и величин в выражение (14):

.

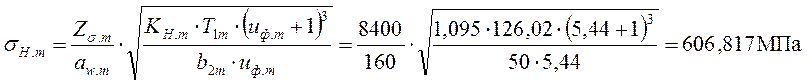Так как s_Н.т < [s]_Н.т (606,817< 644,319), то ранее принятые параметры передачи принимаем за окончательные.

Силы в зацеплении

Окружная сила F_t, кН [1]:

F_t = 2∙10³∙Т₁/d₁ = 2∙10³∙126,02/50,05 = 5,0358 кН.

Радиальная сила F_r, кН [1]:

F_r = F_t∙tg a/Cosb = 5,0358∙0,364/Cos8,482° = 1.8533 кН.

Осевая сила F_а, кН [1]:

F_а = F_t∙ tg b = 5,0358∙tg 8,482° = 0,7508 кН.

Проверка зубьев колес по напряжениям изгиба

Расчетное напряжение изгиба в зубьях колеса [1]:

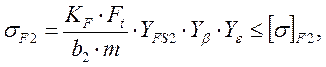                                                                        (15)

где Y_FS2 – коэффициент, учитывающий форму зуба и концентрацию напряжений; Y_b – коэффициент, учитывающий угол наклона зуба в косозубой передаче; Y_e – коэффициент, учитывающий перекрытие зубьев.

Коэффициент Y_FS2, учитывающий форму зуба и концентрацию напряжений выбирается в зависимости от приведенного числа зубьев и коэффициента смещения для внешнего зацепления принимают по табл. 2.10 [1].

Приведенное число зубьев z_v:

z_v1 = z1/cos³b = 33/cos³8,482° = 34.1

z_v2 = z₂/cos³b = 178/cos³8,482° = 183.97