Линия, построенная методом наименьших квадратов. Метод линеаризации данных. Нелинейный метод наименьших квадратов

Расчетно-графичекая работа №2

Основы теории

В науке и инженерной деятельности в результате экспериментов часто получают совокупность точек . Одно из назначений численных методов - определение формулы y=f(x), которая связывает эти переменные, точнее выбор класса допустимых формул, коэффициенты в которых должны быть определены. Существует целый ряд различных типов функций, которыми можно воспользоваться. Часто это основанная на физических опытах математическая модель, которая в дальнейшем будет исследоваться и которая определяет вид функции.

Сначала выделим класс линейных функций вида y=kx+b. В предыдущей работе было показано, как построить полином, который проходит через множество точек. Однако большинство экспериментов проводится на оборудовании, которое надежно дает три или меньше знаков точности. Часто в измерениях присутствует экспериментальная ошибка. Поэтому не обязательно искать функцию, которая точно проходит через точки. Достаточно найти функцию, которая пройдет близко к точкам.

Возможно несколько критериев близости кривой y=f(x) от экспериментальных данных. Для всех необходимо исследование ошибок :

1.  Максимальная ошибка: E(f)=;

2.  Средняя ошибка: ;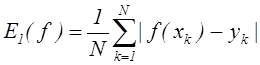

3.  Среднеквадратическая ошибка: .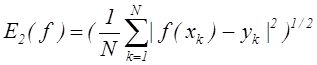

Ясно, что максимальная ошибка наибольшая и если одна точка плохая, то ее значение определяет ). Средняя ошибка - просто среднее абсолютных величин ошибок различных точек. Она часто используется благодаря простоте выведения. Ошибку  часто используют при изучении ошибок статистической природы.

Наилучшая построенная линия определяется путем минимизации одной из величин. Таким образом, можно найти три наилучшим образом построенные линии. Традиционно выбирается третья норма , потому что ее намного легче минимизировать.

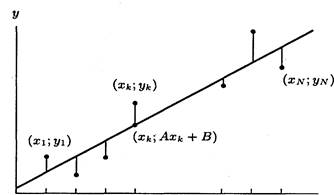
Рис. 1. Расстояния по вертикали между точками {()} и линией, построенной методом наименьших квадратов,у= Ax + В.

1. Линия, построенная методом наименьших квадратов у = Ax + В

Предположим, что {()} - N точек с различными абсциссами {}. Коэффициенты линии, построенной методом наименьших квадратов,

у = Ax + В, являются решениями следующей системы линейных уравнений, известной под названиемнормальные уравнения:

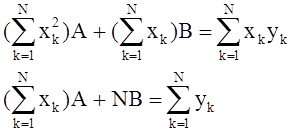
Решаются такие системы уравнений с помощью известных методов решения систем линейных уравнений.

2. Степенная «подгонка» .

В некоторых случаях функция имеет вид , где М - известная постоянная. В этом случае определяем только один параметр А.

Предположим, что {()} - N точек с различными абсциссами точками {}. Коэффициент А кривой, построенной методом наименьших квадратов,  равен

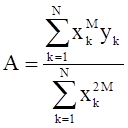
3. Метод линеаризации данных для

Предположим, что заданы экспериментальные точки и требуется найти коэффициенты экспоненциальной функции вида

;

Первым шагом будет логарифмирование обеих частей:

; затем заменим переменные: ;

в результате получим линейное соотношение между новыми переменными X и Y:

Y = AX + В;

Исходные точки  на плоскости xy преобразовались в точки  на плоскости ХY. Этот процессназывают линеаризацией данных. Тогда построенная методом наименьших квадратов линия является наилучшей «подгонкой» к точкам .

Нормальными уравнениями для нахождения А и B будут уравнения

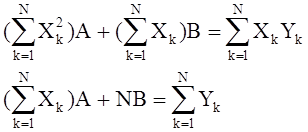
После того как А и В найдены, вычисляем параметр С уравнения: .

Примечание: существуют наборы исходных данных с отрицательными ординатами y, для таких точек провести линеаризацию не представляется возможным. В этом случае следует исключить эти точки из рассмотрения и производить линеаризацию и дальнейшее получение коэффициентов уравнения регрессии по оставшимся точкам.

4. Нелинейный метод наименьших квадратов для

Предположим, что заданы экспериментальные точки и требуется найти коэффициенты экспоненциальной функции вида

Для выполнения процедуры нелинейного метода наименьших квадратов требуется найти минимум функции

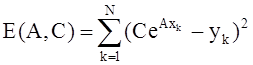
Если положить частные производные равными нулю и затем упростить эти выражения, то можно получить нормальные уравнения:

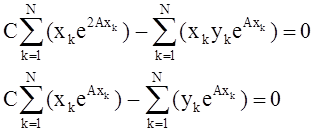
Нелинейные уравнения с неизвестными А и С можно решить встроенными средствами Mathcad. Однако проще непосредственно произвести минимизацию ошибки E(A,C) с помощью встроенной функции Minimize(E,A,C), предварительно задав начальные значения A и С. Фрагмент программы приведен далее:

Указания по выполнению работы

В расчетно-графической работе требуется сравнить различные уравнения регрессии при аппроксимации заданной совокупности точек и выбрать из полученных кривых ту, для которой значение среднеквадратической ошибки минимально (т.е. наилучший вариант). Работа выполняется в среде Mathcad.

Для четных вариантов требуется сравнить следующие случаи:

1. Линейная регрессия (у = Ax + В);

2. Степенная регрессия ();

3. Экспоненциальная регрессия () методом линеаризации данных

4. Экспоненциальная регрессия () нелинейным методом наименьших квадратов.

Для нечетных вариантов:

1. Линейная регрессия (у = Ax + В);

2. Степенная регрессия ();

3. Экспоненциальная регрессия () методом линеаризации данных

4. Экспоненциальная регрессия () нелинейным методом наименьших квадратов.