Моделирование технических систем. Лабораторная работа №1
Двухзонная система подчиненного регулирования
1. Базовая модель
В качестве базовой используем известную модель однозонной двухконтурной системы подчиненного регулирования.
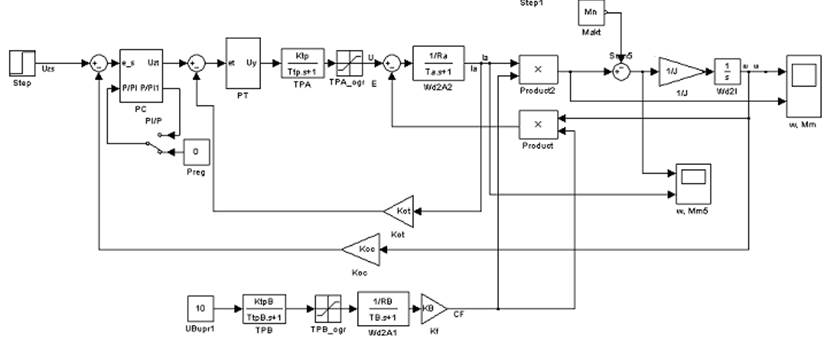 Рис.
1. Пример модели системы подчиненного регулирования с ограничениями
Рис.
1. Пример модели системы подчиненного регулирования с ограничениями
Особенностью модели на рис. 1 является наличие блоков ограничения сигналов регуляторов и управляемого выпрямителя.
2. Параметрическая идентификация модели
Параметры модели двухзонной системы зададим в м-файле:
clear;
% Dvig
U=220; %B
UB=220;
nn1=1000; %об/мин
nn=nn1/60; %об/с
wn=2*3.14*nn;
In=10; %A
lambda=2.5;
kpd=0.9;
B=0.6;
p=2;
iBn=0.12; %A
a=2;
J=0.5; %кг*м^2
Ra=0.5*(1-kpd)*U/In;
CFn=(U-In*Ra)/wn;
Mn=CFn*In;
La=(30/3.14)*B*(U/(p*nn1*In));
Ta=La/Ra;
Tm=(Ra*J)/(CFn*CFn);
Ean=U-In*Ra;
RBn=UB/iBn;
RB=RBn;
LB=(CFn*2*3.14*a)/(p*iBn);
TB=LB/RB;
KB=CFn/iBn;
%ZI
wn=2*3.14*nn ;
wmax=2*wn;
kUzi=10/wn;
%ТП
Ktp=23;
KtpB=23;
Ttp=0.001; %c
TtpB=0.001; %c
%ОС
Uogr=10;
Uogr1=9.56;
Kot=Uogr/(In*lambda);
Koc=Uogr1/(wn*2);
Kon=Uogr/(Ktp*Uogr);
Koe=Uogr1/Ean;
KotB=Uogr1/iBn;
% рег-ры
Krta=(Ta*Ra)/(Kot*Ktp*2*Ttp);
Trta=(Kot*Ktp*2*Ttp)/Ra;
Krca=(Kot*J)/(Koc*4*Ttp*CFn);
Trca=(32*Koc*Ttp*Ttp*CFn)/(Kot*J);
KrtB=(RB*TB)/(2*KotB*KtpB*TtpB);
TrtB=(2*KotB*TtpB*KtpB)/(RB);
Tre=(4*TtpB*Koe*KB)/KotB;
3. Коэффициенты обратных связей
Коэффициенты обратных связей рассчитываются из следующих соображений:
3.1. Максимальное напряжение в системе управления принимаем равным, например, 10 В (самое распространенное). При подаче на вход управляемого выпрямителя (УВ) управляющего сигнала в 10 В, напряжение на его выходе должно равняться максимальному, т.е. 230 В (10*Ktp), т.е. Ktp=23. Практически, это же значение напряжение (Uogr=10 В) является максимальным выходным напряжением для любого регулятора.
3.2. Двигатель развивает номинальную скорость (wn) при номинальном напряжении 220 В (и номинальной нагрузке на валу). Напряжению на выходе УВ равному 220 В соответствует управляющий сигнал напряжением Uogr1=9,56 В (=10*220/230). Таким образом, при сигнале задания на скорость равному 9,56 В двигатель должен развивать номинальную скорость. В этом случае при напряжении управления 10 В, УВ выдает 230 В и система может отработать небольшое (5-6%) перерегулирование по напряжению (относительно номинального). Если предполагается большее перерегулирование, то напряжение задания, соответствующее номинальной скорости выбирается меньшим.
3.3. Исходя из всего вышесказанного, выбирается коэффициент датчика скорости: Koc=Uogr1/wn – для однозонной системы, Koc=Uogr1/(wn*2) – для двухзонной системы, если предполагается, например, достижение удвоенной номинальной скорости.
3.4. Сигнал на входе регулятора тока (ошибка регулирования тока) должен равняться 10 В при максимальном (допустимом) значении тока (In*2,5). Т.е. Kot = Uogr/(In*2,5).
3.5. Аналогично, ток возбуждения равняется номинальному при сигнале задания Uogr1, т.е. KotB=Uogr1/iBn. При этом возможна отработка небольшого перерегулирования или небольшое повышение тока возбуждения и потока. Значительное повышение магнитного потока ДПТ не применяется.
3.6. Коэффициент обратной связи по ЭДС выбирается исходя из того, что номинальной ЭДС соответствует напряжение задания Uogr1, т.е. Koe=Uogr1/Ean.
3.7. Коэффициент обратной связи по напряжению (сигнал используется при вычислении ЭДС) по тем же соображениям Kon=Uogr1/(Ktp*Uogr1).
4. Модель двухзонной системы управления
Структурная схема приведена на рис. 2, а отдельные блоки (подсистемы) на рис. 3. Также применяется ограничение выходных сигналов регуляторов и преобразователей. Ключом PI/P осуществляется переключение между ПИ и П-регулятором, т.е. отключается канал с интегратором. Передаточные функции регуляторов соответствуют стандартным, получаемым при синтезе СПР.
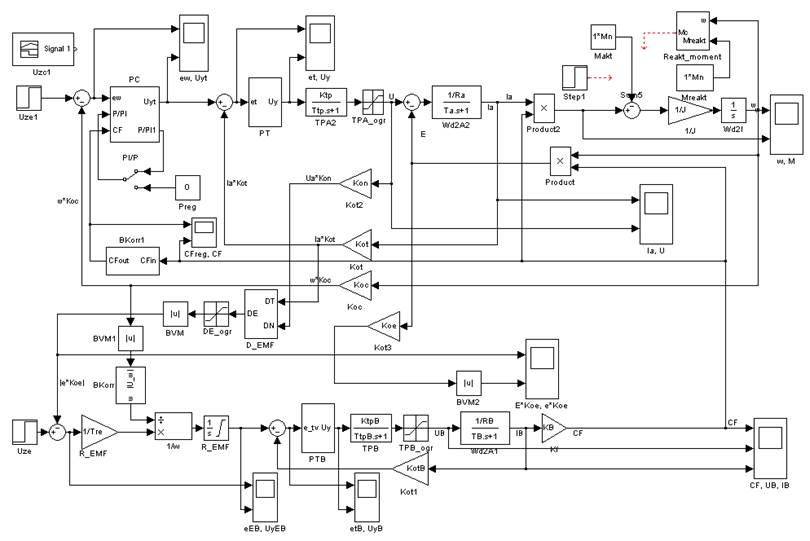
Рис. 2. Структурная схема модели
В регуляторе скорости (рис. 3, а) параметры блока Step (необходим для устранения деления на ноль в начальный момент времени): Step time = 0.0001, Initial value = 1, Final value = 0). Для регуляторов: уровни ограничения в интеграторах и блоках ограничения -Uogr и Uogr, для управляемых выпрямителей Ktp*Uogr, -Ktp*Uogr. Сигнал задания на ЭДС (блок Step Uze): Step time = 0, Initial value = 0, Final value = Uogr1).
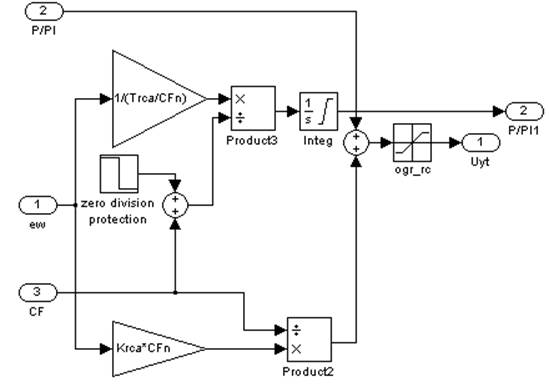
а) регулятор скорости с адаптацией к изменению потока
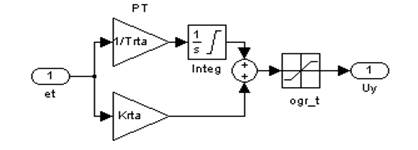
б) регулятор тока якоря
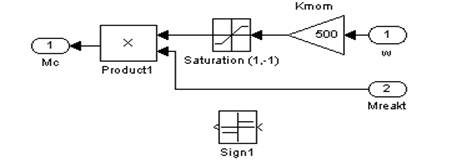
в) схема для получения реактивного момента
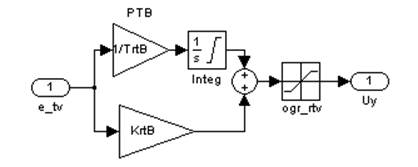
г) регулятор тока возбуждения
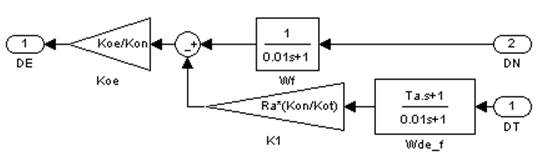
д) датчик ЭДС
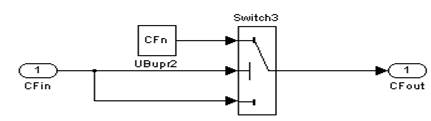
е) блок коррекции значения потока
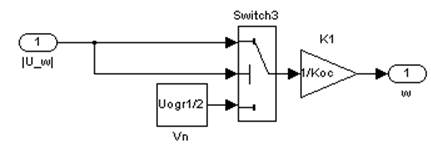
ж) блок коррекции значения скорости
Рис. 3. Подсистемы в составе модели
5. Замечания по модели:
В некоторых случаях требуется изменение постоянных времени фильтров в датчике ЭДС, с целью уменьшения ошибки дифференцирования.
При коррекции передаточной функции регулятора скорости, в данной модели предполагается, что поток измеряется непосредственно. Однако можно создать модель, где поток вычисляется по измеренным значениям ЭДС и скорости. В целом особой необходимости в коррекции передаточной функции регулятора скорости нет, если качество переходных процессов без нее является удовлетворительным. В этом случае сигнал CFn можно подать на регулятор скорости в виде постоянного значения.
Данная модель имеет следующий недостаток: при использовании ПИ-регулятора скорости, в случае если он выходит на ограничение (т.е. при больших сигналах задания), в режиме холостого хода наблюдаются колебания напряжения, тока и момента. В случае П-регулятора такого явления нет. Причина этого скорее в некорректности моделирования ограничений ПИ-регулятора или в наличии вычислительных погрешностей. В некоторых случаях от этой проблемы удается избавиться изменением постоянных времени фильтров в блоке расчета ЭДС или изменением постоянной времени тиристорных преобразователей.
6. Задание. Смоделируем следующие режимы:
1. При работе в первой зоне (сигнал задания на скорость не более Uogr1/2) пуск на холостом ходу (или при небольшой нагрузке), затем наброс максимальной нагрузки в установившемся режиме. Сравним процессы в данном режиме с П- и ПИ-регулятором скорости.
2. Осуществим пуск на номинальную скорость, а затем, через некоторое время после достижения установившегося режима, разгон до удвоенной номинальной скорости. Сравним переходные процессы при работе в таком режиме на холостом ходу и при моменте сопротивления равном номинальному. Сравним время регулирования во второй зоне в этих случаях. Сравним ток двигателя при работе в первой и второй зоне регулирования при одной и той же нагрузке на валу. При какой нагрузке на валу еще возможна работа во второй зоне?
3. Смоделируем работу по тахограмме с ускоренным возвратом при нагрузочной диаграмме, которые показаны на рис. 4.
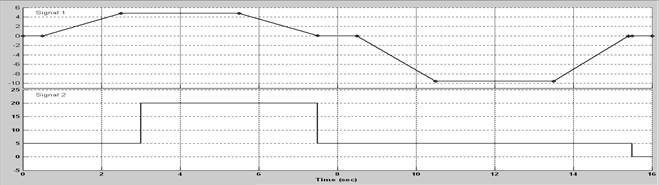 Рис. 4.
Рис. 4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.