Идентификация объекта второго порядка по переходной характеристике. Модифицированный метод Ольденбурга – Сарториуса

Расчетно-графическая работа №1

Идентификация объекта второго порядка по переходной характеристике

Необходимо определить параметры объекта управления с передаточной функцией

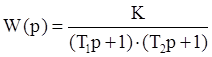 по экспериментальной переходной характеристике h(t).

Для идентификации объекта возможно использование нескольких методов, каждый из которых состоит из определенной последовательности шагов.

1.  Упрощенный метод Орманса

Алгоритм расчета:

1.1  Определить К по установившемуся значению переходной характеристики.

1.2  Найти  из условия   и найти .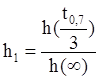

1.3 Вычислить .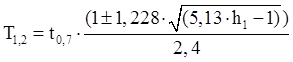

2.  Модифицированный метод Ольденбурга – Сарториуса

Алгоритм расчета:

2.1  Построить график функции  .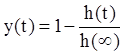

2.2  Определить момент времени , соответствующий точке перегиба и значения функции  у(), y(2).

2.3  Значение =2 соответствует точке пересечения касательной к кривой y(t) в точке перегиба, c осью абсцисс.

2.4  Найти  .

2.5  Вычислить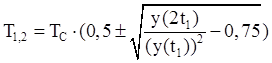 

Нахождение точки перегиба влияет на точность.

3.   Метод моментов

3.1  Вычисляем с помощью метода численного интегрирования (нахождение y(t) см. п. 2.1)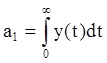 

3.2  Вычисляем значения вспомогательной функции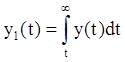

3.3  Вычисляем коэффициент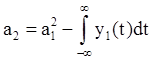 

3.4  Вычисляем 

4.   Метод  последовательного логарифмирования

Алгоритм расчета:

4.1  Построить график функции  у(t)  в полулогарифмическом масштабе, используя по оси t равномерную, а по оси y(t) логарифмическую шкалу.

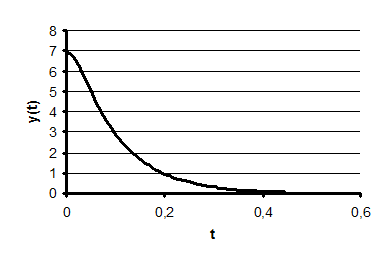
Рис. 1. Пример графиков по п. 4

4.2  При больших значениях  t  аппроксимировать  y(t)  прямой  , где  –координата точки пересечения прямой с осью ординат, а  – тангенс угла наклона к оси абсцисс, и определить  и .

4.3  Ошибку аппроксимации  , построенную также в полулогарифмическом масштабе можно  заменить линейной функцией  .

4.4  Найт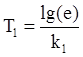и   и 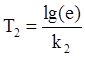. При использовании натуральных логарифмов множитель lg(e) не нужен.

          Содержание отчета по п. 1-4

Отчет должен содержать результаты расчетов по пунктам 1-4 с необходимыми графиками и пояснениями, сравнение полученных результатов, выводы.

Определение параметров двигателя постоянного тока по амплитудно-частотной характеристике

Необходимо определить параметры двигателя постоянного тока, передаточная функция которого 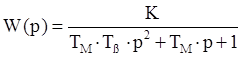 по экспериментальной  амплитудно-частотной характеристике.

Предлагается использовать несколько методов, каждый из которых состоит из определенной последовательности шагов.

5. Метод логарифмической амплитудно-частотной характеристики

5.1. По данным таблицы построить логарифмическую амплитудно-частотную  характеристику.

5.2. Аппроксимировать построенную характеристику отрезками прямых с наклоном, кратным 20 дб/дек.

5.3. Записать выражение для передаточной функции и определить значения параметров.

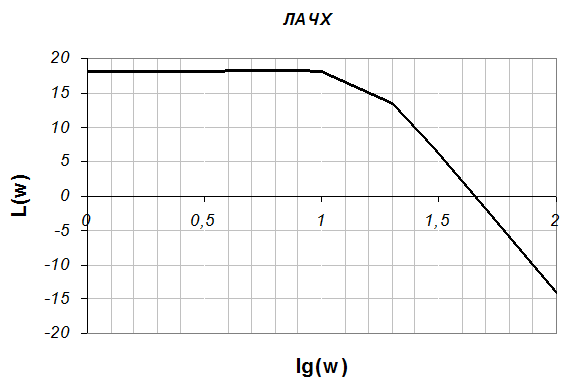
Коэффициент K=20lg(Amax). Аппроксимировав, получим лог. частоты среза. Получим просто частоты 10^w. Затем получим постоянные времени T=2п/wcp.

6. Метод наименьших квадратов

6.1. По данным таблицы вычислить  промежуточную функцию у(w) = 1/ A²(w).

6.2.Убедиться, что у(w) можно представить полиномом  у(w)=а₀+а₁w²+а₂w⁴,    (1)

где ; ; .

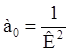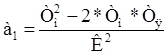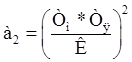6.3. Для n экспериментальных точек составить матрицы (достаточно n=4-5)

             

,

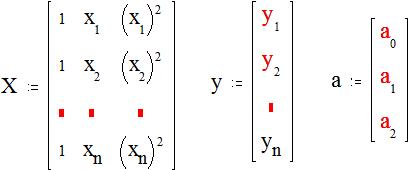
где х_i  = w_i² .

6.4. Определить вектор коэффициентов  а по формуле  

6.5. Найти параметры объекта управления  ; ;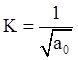

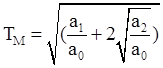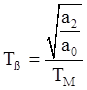
7. Упрощенный метод наименьших квадратов

7.1. По низкочастотной асимптоте логарифмической частотной характеристике определить коэффициент усиления  К.

7.2. В предыдущем методе заменить переменную у новой переменной  z =(K²*y-1)/x

7.3. Убедиться, что (1) преобразуется к виду  z = b₀ + b₁*x, где  b₀ = K²*a₁, а b₁ = K²*a₂.

7.4. Вычислить коэффициенты b0 и b1 по формулам:

åx_i²åz_i-åx_iåx_iz_i

b₀ =  ¾¾¾¾¾¾¾¾ ,

nåx_i² - (åx_i) ²

nåx_iz_i - åx_iåz_i

b₁ =  ¾¾¾¾¾¾¾¾ .

nåx_i² - (åx_i) ²

Эти же коэффициенты можно вычислить и по матричной формуле: b = (X^тX) ^-1X^тz,

в которой матрица Х содержит на один столбец меньше, что облегчает процедуру вычисления обратной матрицы.                           

7.5. Найти параметры двигателя постоянного тока 

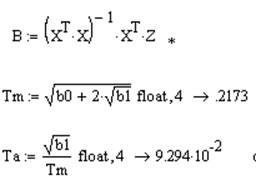
          Содержание отчета по п.5-7

Отчет должен содержать результаты расчетов по пунктам 5-7  с необходимыми графиками и пояснениями, сравнение полученных результатов, выводы.

Исходные данные по п.1-4