Определение параметров двигателя постоянного тока по амплитудно-частотной характеристике. Метод логарифмической амплитудно-частотной характеристики

Определение параметров двигателя постоянного тока по амплитудно-частотной характеристике.

Дано: 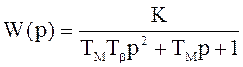, переходная характеристика вариант 3.

Найти: параметры объекта управления.

Решение:

1 Упрощенный метод Орманса

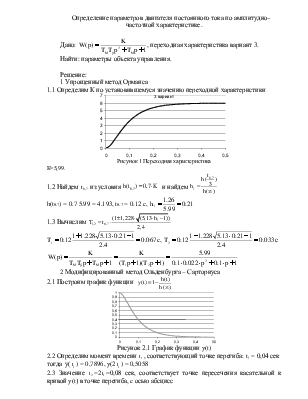
1.1 Определим К по установившемуся значению переходной характеристики

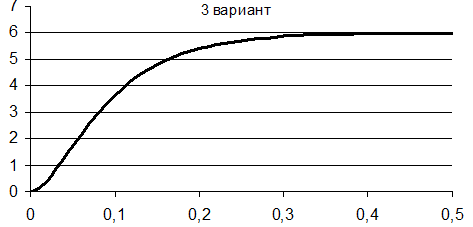
Рисунок 1 Переходная характеристика

К=5,99.

1.2 Найдем  из условия   и найдем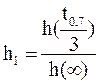

h(t_0.7) = 0.7 5.99 = 4.193, t_0.7 = 0.12 c,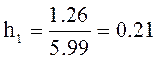

1.3 Вычислим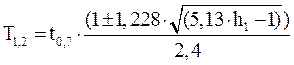

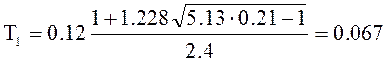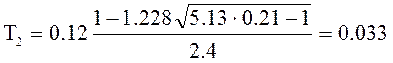c, с

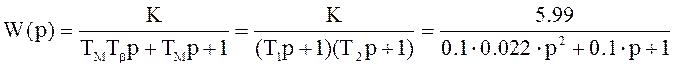
2 Модифицированный метод Ольденбурга – Сарториуса

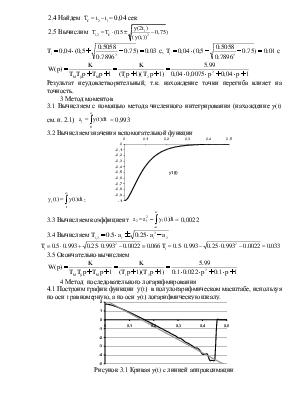
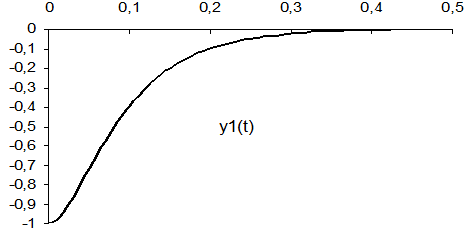
2.1 Построим график функции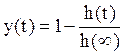 

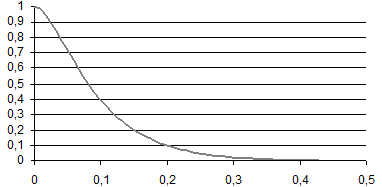
Рисунок 2.1 График функции y(t)

2.2 Определим момент времени , соответствующий точке перегиба: t₁ = 0,04 сек тогда  у() = 0,7896, y(2) = 0,5058

2.3 Значение =2=0,08 сек, соответствует точке пересечения касательной к кривой y(t) в точке перегиба, c осью абсцисс

2.4 Найдем  = 0,04 сек

2.5 Вычислим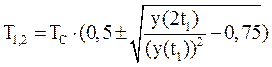 

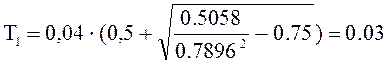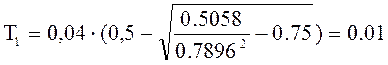 с,  с

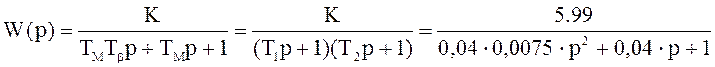
Результат неудовлетворительный, т.к. нахождение точки перегиба влияет на точность.

3 Метод моментов

3.1 Вычисляем с помощью метода численного интегрирования (нахождение y(t) см. п. 2.1) 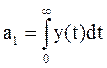  = 0,993

3.2 Вычисляем значения вспомогательной функции

:       

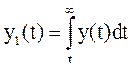3.3 Вычисляем коэффициент 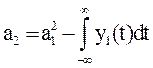 = 0,0022

3.4 Вычисляем

3.5 Окончательно вычисляем

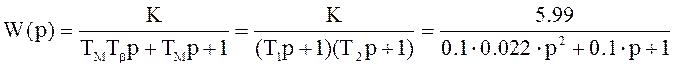
4 Метод  последовательного логарифмирования

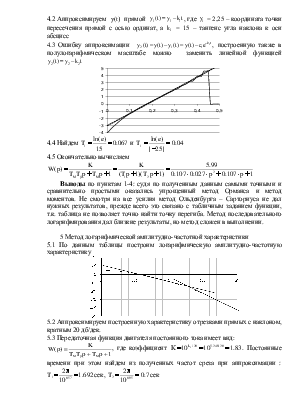
4.1 Построим график функции  у(t)  в полулогарифмическом масштабе, используя по оси t равномерную, а по оси y(t) логарифмическую шкалу.

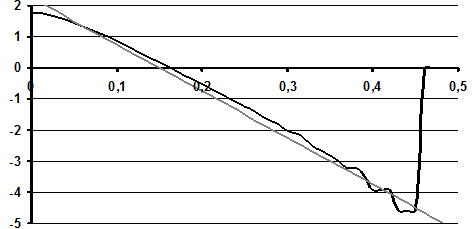
Рисунок 3.1 Кривая y(t) c линией аппроксимации

4.2 Аппроксимируем  y(t)  прямой  , где  = 2,25 – координата точки пересечения прямой с осью ординат, а  = 15 – тангенс угла наклона к оси абсцисс

4.3 Ошибку аппроксимации  , построенную также в полулогарифмическом масштабе можно  заменить линейной функцией 

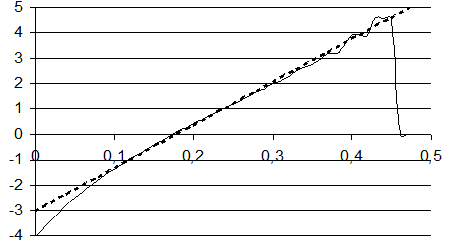
4.4 Найдем 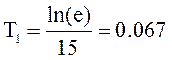 и

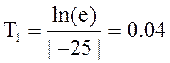
4.5 Окончательно вычисляем

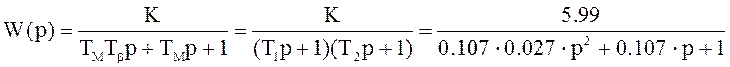
Выводы по пунктам 1-4: судя по полученным данным самыми точными и сравнительно простыми оказались упрощенный метод Орманса и метод моментов. Не смотря на все усилия метод Ольденбурга – Сарториуса не дал нужных результатов, прежде всего это связано с табличным заданием функции, т.к. таблица не позволяет точно найти точку перегиба. Метод последовательного логарифмирования дал близкие результаты, но метод сложен в выполнении.

5 Метод логарифмической амплитудно-частотной характеристики

5.1 По данным таблицы построим логарифмическую амплитудно-частотную  характеристику

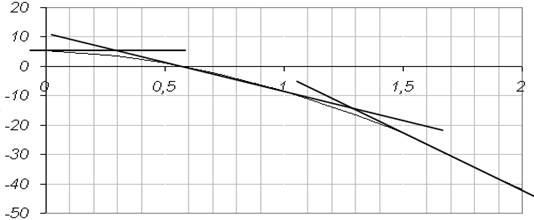
5.2 Аппроксимируем построенную характеристику отрезками прямых с наклоном, кратным 20 дб/дек.

5.3 Передаточная функция двигателя постоянного тока имеет вид:

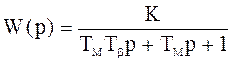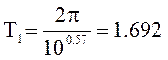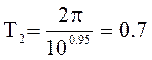, где коэффициент . Постоянные времени при этом найдем из полученных частот среза при аппроксимации : сек, сек

6 Метод наименьших квадратов

6.1 По данным таблицы вычислим  промежуточную функцию у(w) = 1/ A²(w)

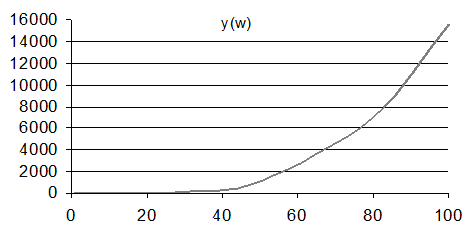
6.2 Представим y(w) в виде полинома  у(w)=а₀+а₁w²+а₂w⁴ , где

, ,

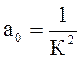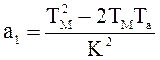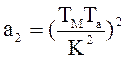
6.3 Для 4 экспериментальных точек составим матрицы

,где х_i  = w_i²

6.4 Найдем параметры объекта управления

7 Упрощенный метод наименьших квадратов

7.1 По низкочастотной асимптоте логарифмической частотной характеристике определим коэффициент усиления  К=1,83

7.2. В предыдущем методе заменим переменную у(w) новой переменной  z(w) = =(K²y(w) -1)/x

7.3. Получим соответственно z(w) = b₀ + b₁x, где  b₀ = K²a₁, а b₁ = K²a₂.

7.4. Вычислить коэффициенты b₀ и b₁ матричным способом

7.5 Найдем параметры двигателя постоянного тока 

Выводы по пунктам 5-7: при выполнении работы равных результатов получено не было, поэтому судить о точности того или иного метода трудно. Имея под рукой средства вычислительной техники, данные методы, не являются трудоемкими.