Итерационные алгоритмы улучшения начального значения. Алгоритм парных перестановок. Алгоритм Штейнберга

Очередной элемент тот, у которого C_j максимально.

 

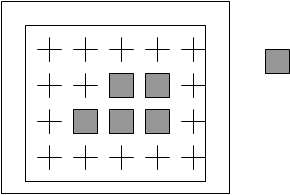Размещенный элемент

l_j пробуется последовательно во всех позициях в рамке (на рис. Обозначены «+»). В качестве результирующей выбирается та позиция, которая дает минимальную длину связи

Достоинства: Простота

Недостатки: Ищет локальное (только для одного элемента) лучшее решение.

Особо оговаривается правило размещения ядра E_k (максимально связанные 1 – 4 элемента помещаются в центр)

3. Итерационные алгоритмы улучшения начального значения

            Алгоритм парных перестановок.

Критерий замены мест – min max l_ij. Для каждой пары l_il_j определяем l_ij. Для max l_ij меняем элемент l_i с соседним, чтобы он стал ближе к l_j. Если количество максимумов уменьшилось или максимум уменьшился, то берем новое размещение, иначе восстанавливаем предыдущее и пробуем другой вариант. В зависимости от начального расположения удается получить от 1 до 50 % причем основное улучшение – за 5 итераций.

Алгоритм Штейнберга

W = {l₁, l₂, …, l_k } – внутренне устойчивое множество (элементы в нем не связаны, а значит, положение каждого из них не влияет на других)

А_ij – суммарная длина связей элемента l_ij на позиции p_ij.

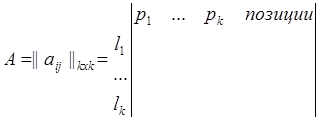Повторить для всех внутренне устойчивых множеств.

Трудоемкость – m³ (max |W| = m)

4. Непрерывно-дискретные алгоритмы

Изначально нет позиция, а только непрерывное поле. Элементы – мат. Точки, на которые действуют силы F_ij притяжения и j_ij отталкивания.

Для каждого элемента составляется СДУ движения точки в положение равновесия. После решения получаем координаты точек, которые потом «натягиваются» на сетку с минимальным искажением.

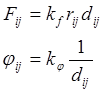Недостатки:  - подбор коэффициентов k_f и k_j

- сложность решения СДУ

Размещение разногабаритных элементов

Различают размещение элементов кратных размеров и существенно разных габаритов. В первом случае – задача целочисленного программирования с ограничениями (в одной позиции могут находиться несколько элементов или один элемент на нескольких позициях)

Один из подходов: дихотомия

Все множество элементов разбивается на 2 малосвязанных подмножества. Площадь, занимаемая элементами 1го подмножества S(E₁), 2го – S(E₂)

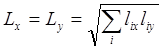S(E₁)+S(E₂) = L_xL_y=S

|S(E₁)-S(E₂)| £ e

Исходная площадь делится пополам:

 

Далее повторяем с каждой из половин до тех пор, пока каждая из частей не будет элементом.

Непрерывно-дискретные методы не используются для большого количества элементов из-за своей сложности.

Алгоритмы трассировки межсоединений

Задача геометрического построения на поле всех цепей данного конструктив., координаты начала и конца которых определены при размещении, с ограничениями:

-  разрешено r проводников или нет

-  возможен переход со слоя на слой

-  сколько слоев для трассировки

-  под каким углом можно проводить проводник

-  допустимая ширина проводников и расстояние между ними

-  максимальная длина двух соседних параллельных проводников.

Алгоритмы зависят от конструктивно-технологической базы и технологии изготовления.

Технология	Критерий
Проводной монтаж Двухстор. ПЛ, многосл с МСО МПП с ОКП (откр. КП) ГИС БИС	Сумм. длина соединения, max lij СДС, число межслойных переходов СДС, число слоев Площадь, число пересечений проводников Площадь, число межслойных переходов

Задачу трассировки межсоединений обычно делят на подзадачи?

1. Что? 2 Где? 3 Когда? 4 Как?

1.  Построение списка соединений

2.  Определение слоя (задача расслоения)

3.  Определение порядка трассировки

4.  Алгоритм трассировки

1.  Построение списка соединения

Сводится к построению минимального связывающего дерева

Алгоритм Прима:

1)  Для любой вершины xi ищется ближайшая к ней, они соединяются

2)  Из всех неприсоединенных ищется ближайшая к этой паре и т.д. до тех пор, пока ребер не станет m-1

Алгоритм Коскала:

Все пары элементов упорядочиваются по неубыванию расстояния между ними. В дерево включается каждое ребро, не образующее цикла с ребрами, уже вошедшими в дерево. Оба алгоритма дают точный результат за полиномиальное время

По Приму:

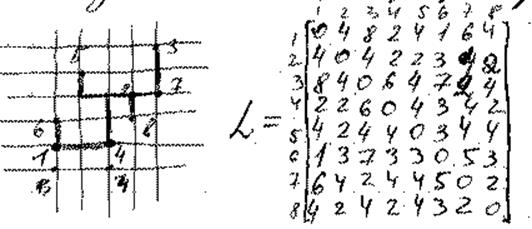1-6; 4-1; 2-4; 5-2; 7-2; 3-7; 2-8

Порядок!!!

По Каскалу:

1-6; 1-4; 2-4; 2-5; 2-7; 2-8; 3-7; 4-8; 7-8

V     V     V    V    V     V     V     X    X

3. Определение порядка трассировки

(порядок проведения соединений)

Порядок влияет на качество трассировки

Метод прямоугольников

Для каждой цепи строится минимальный охватывающий прямоугольник. Подсчитывается количество контактов других цепей, попавших в прямоугольник. Цепи упорядочиваются по неубыванию этого числа. Получившийся порядок – порядок проведения соединений

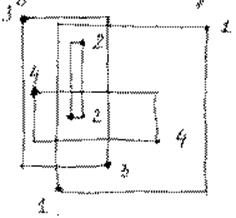Цепь	N
1-1 2-2 3-3 4-4	4 0 3 1

Порядок соединений: 2-2; 4-4; 3-3; 1-1

Можно проводить: короткие-длинные или длинные-короткие

Алгоритм трассировки – основной и наиболее трудоемкий этап, обеспечивающий эффективность и качество трассировки в целом.

Волновой алгоритм и его модификации

Входят во все САПР, предложен Ли.

Коммутационное поле разбивается на дискреты, в кот. Может проходить только один проводник (определяется минимальной шириной проводника и минимальным расстоянием между ними) -> дискретно-рабочее поле ДРП.

Алгоритм состоит из двух этапов:

1) распространение волны 2) проведение трассы

1) Формируются фронты – множество ДРП, входящих в окресность источника А. Распространение волны продолжается до тех пор, пока очередной фронт не достигнет приемника или в него не удается вложить ни одной новой ячейки