 |
2) От ячеек k-го фронта переходим по определенным правилам к k-1 и т.д. до P0. Пройденные ячейки – искомый путь. Пусть критерий – min СДС, тогда пометка: Pi=i, ищем ячейку с Pi-1: Pi=i=Pi-1+1
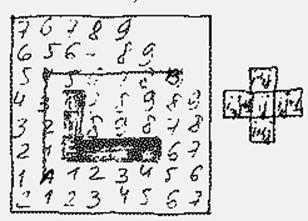 |
Недостатки: в процессе распространения волны каждая ячейка может быть свободна/запрещена/помечена. При max L небоходимо хранить (L+2) значений, т.е. N=log2(L+2) бит информации. Например, для платы 100х100 мм2 и размере дискрета 0,5 (0,2+0,1) ДРП= 200х200 = 40000 ячеек; L=400; N=log2402 = 9, Т.е. каждый дискрет занимает 9 бит. Следовательно потребуется большой объем памяти для хранения ДРП..
Модификация. Кодирование по mod3
Хранится не само число (вес ячейки), а число mod3.
Ячейка: свободна/запрещена/помечена - 0/1/2, т.о. для каждой ячейки храним три бита. И это число не зависит от размера платы.
 |
 |
Для того, чтобы идти в правильную сторону, у любой ячейки должны быть разные соседи. Для этого последовательность 001100110011
N=log24 = 2 бита
На самом деле ячейки сложнее – есть еще признак цепи: если принадлежит цепи, то ячейки помечаются тем же фронтом
Второй недостаток – трудоемкость алгоритмов.
Методы:
1. Выбор источника волны
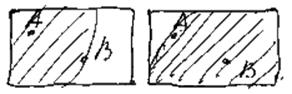 |
За источник волны выбирается ячейка, находящаяся ближе к краю коммутационного поля
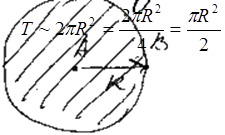
2. Метод встречной волны
 |
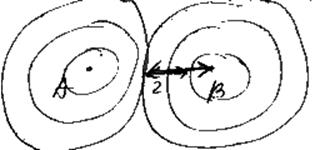 |
3. Обрамление
 |
Главные недостаток – последовательный характер алгоритма. Учет длины пути, числа переходов со слоя на слой необходим:
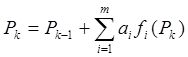 |
Пример: Пусть учитываются 2 параметра: СДС и количество переходов:
а1 = 1; f1 = 1
а2 = 3; f2 = 1, если есть переход, 0, если нету
DР = 1+3f2
 |
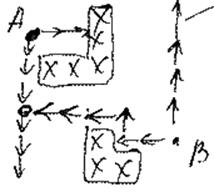
Для пути: l=11, количество переходов n=3
Для пути (кратчайшего): l=7; n=5.
Основной луч
 |
 |
 |
Скорость на два порядка выше, чем у волнового.
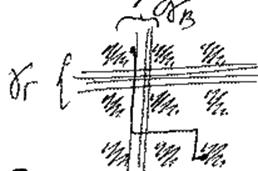
gГ – емкость горизонтального канала; gВ – вертикального (максимальная)
1. Распределение соединений по каналам
2. Распределение соединения по магистралям
 |
g
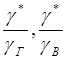 |
2)
 |
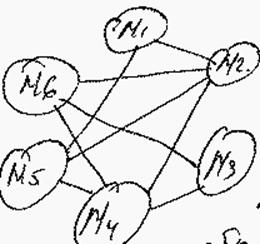 |
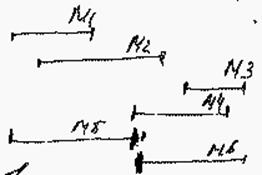
M1,M5,M2,M4,M6,M3
Просматривая последовательность слева направо, помещаем интервалы на как можно более верхнюю магистраль так, чтобы они были несмежны в графе:
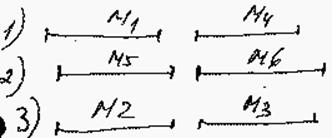 |
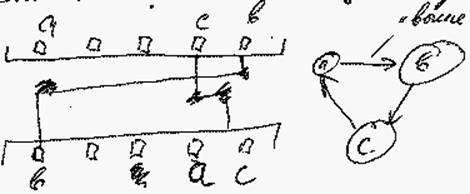 |
Если возможно, то трасса проводится слева как можно выше. Когда все проведено, там, где не мешают друг другу, спрямляют.
Достоинства: Скорость на 1-2 порядка выше, чем у волнового.
Не нужно хранить все ДРП
Проводники проводятся с учетом следующих на обоих этапах
Недостатки: Используется только для регулярных структур
Пусть задан граф G(X,U), ребрам которого предписаны веса C = ||Cij||
Задача о кратчайшем пути состоит в нахождении пути с минимальным суммарным весом от начальной вершины SÎX до конечной tÎX или до всех остальных, если такие пути существуют.
Для случая Cij³0. Основан на приписывании вершинам временных пометок – верхняя граница длины пути от S к этой вершине. Эти пометки постоянно уменьшаются, и на каждом шаге ровно одна вершина получает постоянную (+) пометку – минимальная длина пути от S к этой вершине.
l(xi) – пометка вершины xi
1. l(s)=0+
l(xi) = ¥; xj ¹S, xj Î X
p – вершина, последняя получившая постоянную пометку p=S.
2. Для всех вершин xj Î Гр смежных с последней вершиной р и имеющих временные пометки уточняется временная пометка:
L(xj) = min [ l(xj), l(p)+C(pxj) ]
3. Из всех вершин, имеющих временную пометку, выбирается вершина с
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.