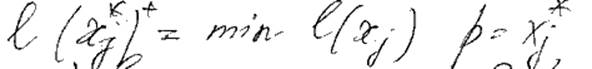
4. а) Если ищем путь S - t проверяется: p = t ? Если нет, то goto 2. Else кратчайший путь найден.
б) Ели ищем путь от S, ко всем остальным вершинам. Все ли вершины имеют постоянную пометку? Если нет то goto 2. Else пути определены. Путь определяется с.о.:
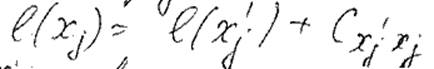
X ’ j – вершина непосредственно предшествующая вершине X j в кратчайшем путе.
Сложность алгоритма O( n log 2 m), n = | V |, m = | X |
Найти кратчайшие пути от X1 до всех остальных.
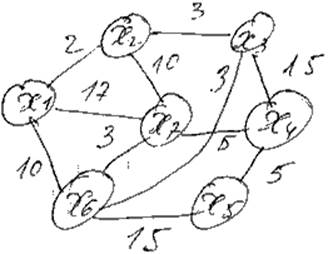
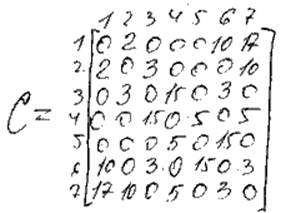
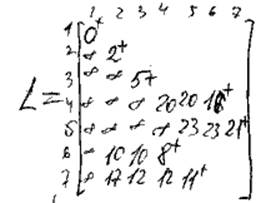
1) L( X1 ) =
0+, L( Xj ) = ![]() , P = X1
, P = X1
2) Гр = { X2, X6, X7 }
L( X2 ) = min[![]() , 0 + 2 ] = 2
, 0 + 2 ] = 2
L( X6 ) = 10
L( X7 ) = 17
3) L( X3 ) = min L( Xj ), P = X2
4) Гр = { X1, X3, X7 }
L( X3 ) = min
[![]() , 2 + 3 ]
= 5
, 2 + 3 ]
= 5
L( X7 ) = min [ 17, 2 + 10 ] = 12
5) L( X3 ) = min, P = X3
6) Гр = { X2, X4, X6 }
L( X4 ) = 5 + 15 = 20
L( X6 ) = min [ 10, 5 + 3 ] = 8
7) P = X6
Гр = { X1, X3, X5, X2 }
L( X5 ) = 8 + 15 = 23
L( X7 ) = min [ 12, 8 + 3 ] = 11
8) P = X7
Гр = { X1, X2, X4, X6 }
L( X4 ) = min [ 20, 11 + 5 ] = 16
9) P = X4
Гр = { X3, X5, X7 }
L( X5 ) = min [ 23, 21 ] = 21
Пути:
X5 X4 C X4 X5 X4 X7 C X4 X7
21 = 16 + 5 16 = 11 + 5 и т.д.
1) Самый надежный путь.
Ребрам присваивается надежность p( XiXj ).
Надежность пути равна
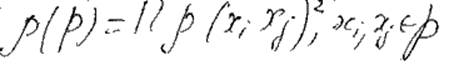
2) Самый длинный путь.
3) Путь с наибольшей пропускной способностью.
У ребер qij
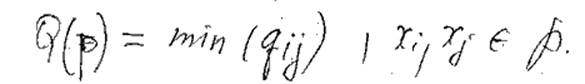
Если
все вершины графа разбить на два подмножества Xs и Xt, то множество ребер графа одна
![]() вершина
вершина ![]() , а вторая
, а вторая ![]() над
разрезом графа.
над
разрезом графа.
Теорема.
Пропускная способность пути с наибольшей пропускной способностью равна
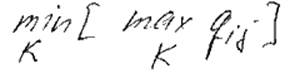
Где К – любой S – t разрез графа.
Для неорграфа разработан алгоритм Франка-Фриша
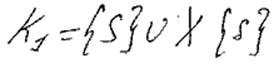
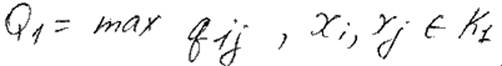
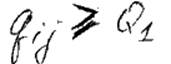
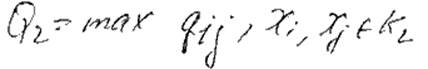
goto 2
4) Пока S и t не будут закорочены. Qk – это и есть max преп. сп-ть.
Для нахождения самого пути строится граф
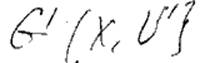 V – закороченные
ребра.
V – закороченные
ребра.
![]() путь в построенном
графе является путем с max пропускной способностью.
путь в построенном
графе является путем с max пропускной способностью.
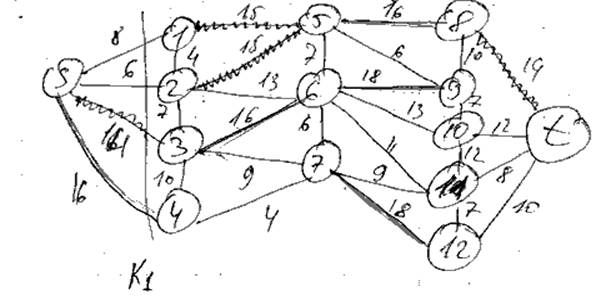
1) max qij = 16 = Q1
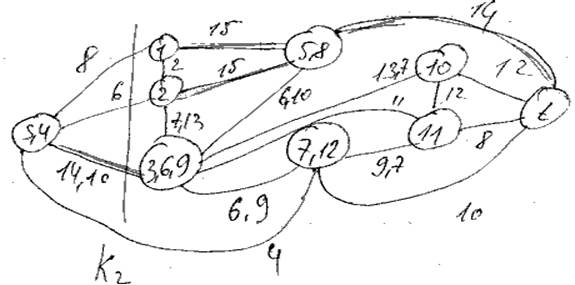
2) Q2 = 14
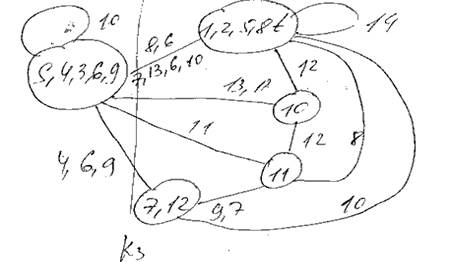
3 ) Q3 = 13
1) 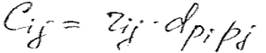
Найти кратчайшее
расстояние от ![]() угловой вершины до
всех остальных.
угловой вершины до
всех остальных.
2) ![]()
Найти путь с наибольшей пропускной способностью по диагонали.
Алгоритмы трассировки.
Алгоритм Винтера ( 1984 )
Недостатки волновых алгоритмов – послед. характер, возможного замуровывания выводов.
Винтер предложил алгоритм с многократным повторением шага построения всех трасс.
На каждом шаге сохраняется только часть трасс.
SPECCTRA – автотрассировщик
В нем используется бессеточный алгоритм. На первом шаге проводятся все соединения без ограничений. На каждом шаге трассировщик пытается уменьшить количество конфликтов. Используется 2 метода:
- DASH-AND-SHORT – вставка и рассталкивание
- RID-APP-ADD-RETRY – развертывание и проталкивание
Ни один алгоритм не может обеспечить 100% разводки, поэтому постоянно необходимо дорабатывать. Требование: простая конфигураци трасс.
Последовательные алгоритмы компоновки.
Компоновка – разбиение исходных схем на подсхемы.
Сводится к разбиению графа G( X, V ) на части G1( X1, V1 )… GN Xn Vn), т . е., чтобы
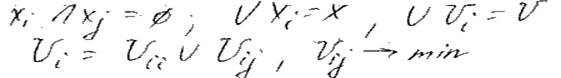
1) Для все вершин Xi определяется степень p( Xi ) и выбирается вершина с min степенью.
Если таких вершин нет, то выбирается вершина с наибольшем количеством кратных ребер.
2) В первый кусок включается вершина Xi и вершины смежные с ней. ![]()
3). а) В первом куске оказалась | X1| = n1 вершины -> end
б) |X1| > n1 для всех Xj Э X1 выбирается вершина min связанная с вершинами первого куска, она удаляется из первого куска.
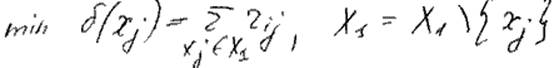 goto а).
goto а).
в) |X1| < n1. Для ![]() выбирается вершина max связанная с вершинами X1( max б/Xj ); X1 = X1 U { Xj } goto а).
выбирается вершина max связанная с вершинами X1( max б/Xj ); X1 = X1 U { Xj } goto а).
5) X = X \ X1 goto 1). до тех пор пока не сформирован Xn-1 кусок.
2. 1) Для всех Xi определяем p( Xi ) и выбираем p( Xi ) = min X1 = { Xi }
2) Для всех ![]() вычисляем
вычисляем
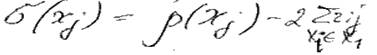
3) Выбираем 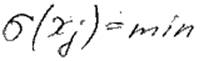
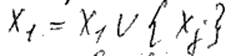
2), 3) повторять пока | X1 | = n1, затем пока не сформирован Xn-1
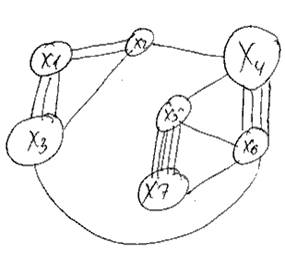
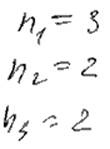

1. 1) X1 = { X2 } U { X1, X3, X4 } \ X4 = { X1, X2, X3 }
2) X2 = { X4 } U { X5, X6 } \ X5 = { X4, X6 }
3) X3 = { X5, X7 }
2.
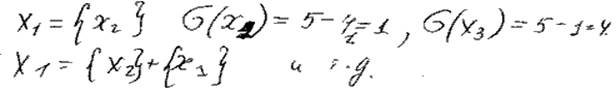
Алгоритм обратного размещения.
E = { E1, E2, … , Em }, P = { P1, P2, … , Pk }, m <= k
элементы позиции
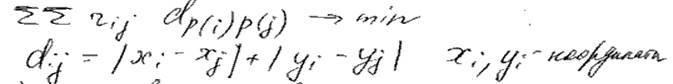
Оцениваются все элементы и все позиции.
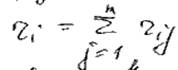 количество связей i-того элемента
количество связей i-того элемента
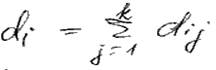 суммарное расстояние
от i-той позиции до все остальных
суммарное расстояние
от i-той позиции до все остальных
2) Все элементы упорядочиваются по убыванию. Все позиции – по возрастанию.
Если m < k то лучше все наоборот.
4) Все элементы размещаются на соответсвующие позиции 
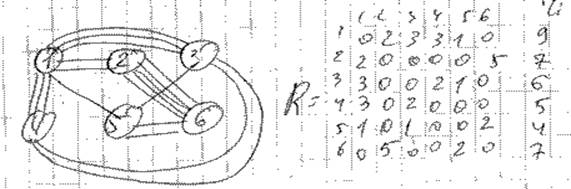

L5 L4 L3 L2 L6 L1
P1 P6 P4 P3 P2 P5
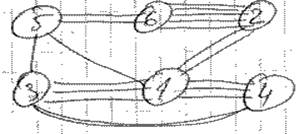
Точное решение.
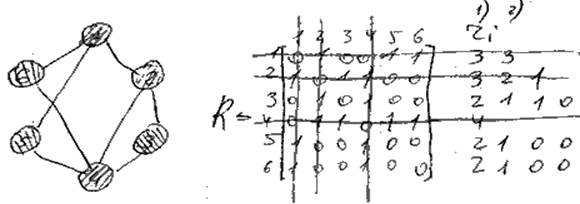
Алгоритм расскраски графов.
Расскраской графа называется разбиение множества вершин графа на подмножества, т. е. чтобы в каждом из подмножеств вершины были не смежны.
1) Построить все max устойчивые множества.
2) Выбор min их количества для покрытия всех вершин ( метод Петрикса)
1. 1) Д/Xi рассчитываем ri – кол-во нулевых связей.
2) Выбираем max ri.
3) Удаляется вершина Xi и инцендентные ей ребра ( удаляем из матрицы R строку и столбец)
4) Если R != 0, то переходим к п. 1
5) П = С1 С2 ... Сk = минимизация = Vkj Kj = Xa, Xb, …
6) Для каждого Kj строится Фj, в которую входят вершины не вошедшие в Kj
Фj – max внутренее устойчивое множество.
2. 7) Для каждой Xi строится ti = VФj, Фj – множество в кот. входят вершины.
8) П’ = ti t2 … минимизация
9) ![]() - ДНФ
- ДНФ
Выбираем терм содержащий min кол-во сомножителей ( это хроматическое число графа )
Каждое Фj, вошедшее в этот терм – множество вершин которые м.б. окрашено одним цветом.
Если термов несколько => существует несколько вариантов раскраски.
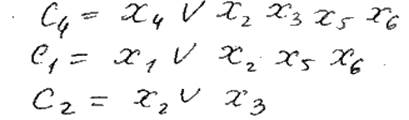
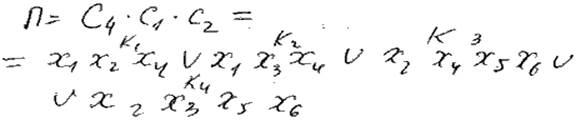
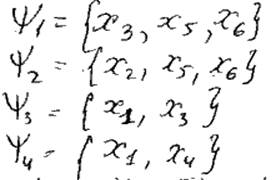
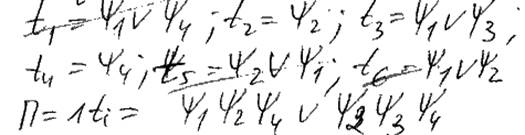
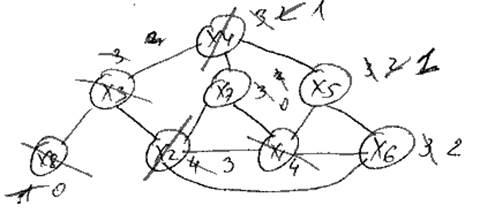
Приблеженные алгоритмы расскраски.
Алгоритм с упоряды\очиванием.
1) Пусть цвет j = 1
2) Для каждой Xi подсчитываем ri
3) Вершины упорядочиваются по невозрастанию ri
4) Просматривая последовательность, в цвет j красится вершина не смежная с уже окрашенными в этот цвет.
5) Если не все вершины окрашены, из графа удаляются окрашенные вершины,
j = j + 1, goto 2
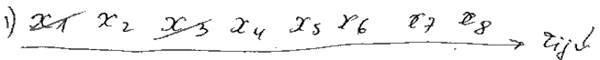
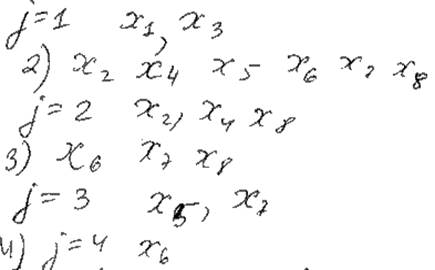
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.