Одновременно строится граф пересечений G`
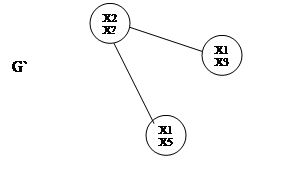 |
Для определения двудольности используется максимальные внутренне устойчивые множества (их можно построить методом Магу)
Алгоритм П.
|
1 |
2 |
3 |
4 |
||
|
v |
1 |
1 |
0 |
1 |
0 |
|
2 |
0 |
1 |
. |
. |
Выделение из графа пересечений G` макс. двудольного подграфа H`
Для этого введем следующий критерий:
αγδ= |Ψγ| + |Ψδ| - |Ψγ∩Ψδ|
Если αγδ= |Ψγ| + |Ψδ| = |X`| , т.е. |Ψγ∩Ψδ| = 0, то граф G` двудольный и планарный.
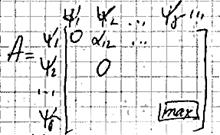 Если это не так, то чем
αγδ ближе к
к |X`|, тем большее число ребер содержи выделенный
двудольный граф, т.е. необходимо найти такие γ и δ, которые дают максимальный αγδ.
Если это не так, то чем
αγδ ближе к
к |X`|, тем большее число ребер содержи выделенный
двудольный граф, т.е. необходимо найти такие γ и δ, которые дают максимальный αγδ.
Максимальному H` в исходном графе G соответствует суграф H, содержащий максимальное число непересекающихся ребер.
![]() =>
=> ![]() ,
, ![]() и т.д
и т.д
Причем матрица ![]() получается
из матрицы RG`
вычеркиванием строк и столбцов, соответствующих вершинам, попавшим в Ψγ и Ψδ.
получается
из матрицы RG`
вычеркиванием строк и столбцов, соответствующих вершинам, попавшим в Ψγ и Ψδ.
![]() получается из ΨG`, выкинув вершины, вошедшие в Ψγ и Ψδ и объединив одинаковые.
получается из ΨG`, выкинув вершины, вошедшие в Ψγ и Ψδ и объединив одинаковые.
Итого:
Пример:
Граф, что и в предыдущем примере. Преобразуем: (перенумеруем вершины)
![]() x1 x2 x3 x5 x6 x7 x4
x1 x2 x3 x5 x6 x7 x4
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Pi |
||
|
R= |
1 |
0 |
+ |
1 |
0 |
0 |
0 |
+ |
0 |
|
2 |
0 |
+ |
1 |
0 |
1 |
0 |
2 |
||
|
3 |
0 |
+ |
1 |
1 |
1 |
4 |
|||
|
4 |
0 |
+ |
0 |
1 |
3 |
||||
|
5 |
0 |
+ |
1 |
2 |
|||||
|
6 |
0 |
+ |
|||||||
|
7 |
0 |
||||||||
|
P(G) = 11 |
x1 x2 x3 x4 x5 x6 x7
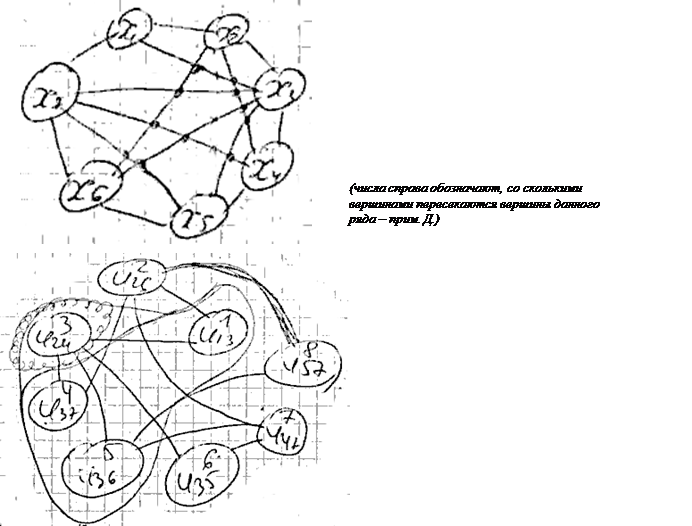
Если гамильтонова цикла нет, то строим цепь и достраиваем до цикла, добавляя одно или несколько псевдоребер.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
||||
|
R= |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
||
|
2 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|||
|
3 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|||
|
4 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|||
|
5 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|||
|
6 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|||
|
7 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|||
|
8 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
I = 1 ; r1 v r4 = M14 = 11110000
M145 = 11111011
M1456 = 11111111
r1 v r7 = M17 = 11101110
M174 = 11111110
M1748 = 11111111
I = 2 ; r2 v r3 = M23 = 11111111
r2 v r5 = M25 = 11111011
M256 = 11111111
|
I=3; r3 v r7 = M37 = 11111110
M378 = 11111111
|
A= |
Ψ1 |
Ψ2 |
Ψ3 |
Ψ4 |
|
|
|
Ψ1 |
0 |
6 |
6 |
5 |
7 |
|
|
Ψ2 |
0 |
6 |
7 |
6 |
||
|
Ψ3 |
0 |
4 |
4 |
|||
|
Ψ4 |
0 |
6 |
||||
|
Ψ5 |
0 |
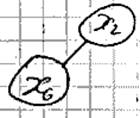
G` \ H = {X2, X6}
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.