Исследование влияния температуры на натяжение и стрелы провеса проводов. Изучение состояния свободно подвешенного провода

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ № 3.

«ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕМПЕРАТУРЫ НА НАТЯЖЕНИЕ И СТРЕЛЫ ПРОВЕСА ПРОВОДОВ»

Выполнили:

Проверил:                                                                             

Санкт-Петербург

2007

Лабораторная работа № 3.

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕМПЕРАТУРЫ НА НАТЯЖЕНИЕ

И СТРЕЛЫ ПРОВЕСА ПРОВОДОВ

Цель работы – изучение зависимости стрел провесов и натяжений проводов, а также работы полукомпенсированной контактной подвески в пролёте при измени натяжения несущего троса.

Краткие теоретические сведения

На электрических железных дорогах применяются простые ( однопроводные) и цепные контактные подвески. Исследованию зависимости изменения стрел провесов проводов контактных подвесок от температуры посвящена данная работа.

Абсолютно гибкая нить, например, цепочка, провисает по цепной линии, уравнение которой у=m•ch•x/m ,                                                                                                   (3.1)

где m=Н/g

н - горизонтальная составляющая натяжения, даН;

g - нагрузка от силы тяжести, даН/м.

При относительно малых провесах можно считать, что вес проводов распределен не по длине нити, а по длине пролета. Тогда рассматривая равновесие половины пролета провода, можно получить простые формулы для опредения провеса и натяжения провода, провисающего по параболе (рис.1).

I=4.8

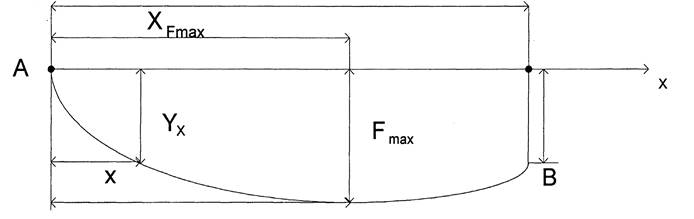
Рис.1.Схема модели

Сумма моментов всех сил относительно точки С

Мх—Н•у=о                                                                                                 (3.2)

откуда провес у=Мх/Н                                                                                                        (3.3)

Длина провода в отрезке может быть определена по формуле длины параболы. Длина отрезка одной ветви параболы от вершины О до точки с координатами (х, у)

Lx=х+2/3 • /x                                                                                          (3.4)

Тогда при х = 0,5 • l и у =f:

L0,5l=l/2+4/3 •/l                                                                                      (3.5)

Тогда длина обеих ветвей параболы, т.е. длина провода в пролете:

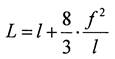                                                                                                 (3.6)

Выразив f через q и Н получим:

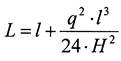,                                                                                              (3.7)

При изменении температуры и нагрузки, например, при образовании гололеда длина провода изменяется. Зная законы температурного и упругого удлинений, можно написать уравнение состояния провода над длиной пролета для любого режима. Удлинение провода при переходе из состояния с параметрами t1, q1, H1 к состоянию tх, q х, Hх :

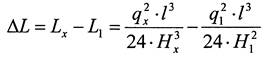                                                                        (3.8)

Зная коэффициент температурного удлинения а, модуль упругости материала Е и сечение провода S , из (3) получим

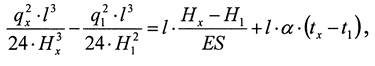                                                     (3.9)

Разделив уравнение на al, напишем его в виде, удобном для решения

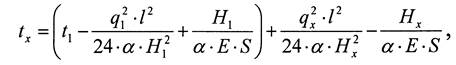                                       (3.10)

Задаваясь натяжением Hx, можно определять температуру tx или наоборот. По аналогии можно получить формулы для цепной подвески.

Лабораторная работа № 3.1.

Содержание работы

На моделях подвесок устанавливаются различные режимы их состояния.

Замеряются фактические провесы и натяжения, которые затем сравниваются с расчётными.

Поскольку в лаборатории трудно осуществить изменение температуры, то при проведении этой работы изменяется натяжение провода путём изменения натяжения соответствующих проводов, и по уравнению состояния определяется температура, соответствующая этому натяжению.

Порядок выполнения работы № 3.1

1 .Изучение состояния свободно подвешенного провода.

а) В соответствии с вариантом задания задаём провода б) Через каждые 100 мм с помощью линейки определяется стрела провеса провода от опоры 2 к опоре З (от более высокой точки подвески к натяжение более низкой).

в) Замеряем провесы и замеряем разность уровней  Dh на опоре З (по осям проводов). Полученные данные заносим в таблицу 1.

г) По приведённым формулам вычисляется расчётным путём провес провода в тех же самых точках, что и при физическом опыте. Данные заносятся в табл.1, в таблице вычисляется разность между фактическими и расчётными значениями каждой точки.

д) Расчётным путем находим расстояние от опоры 2 до нижайшей точки провода в пролёте и рассчитываем его по приведённым формулам. Расчёты заносим в табл.1 и производим расчёт отклонений (как разницу между фактическим и расчётным значением).

Рабочие формулы:

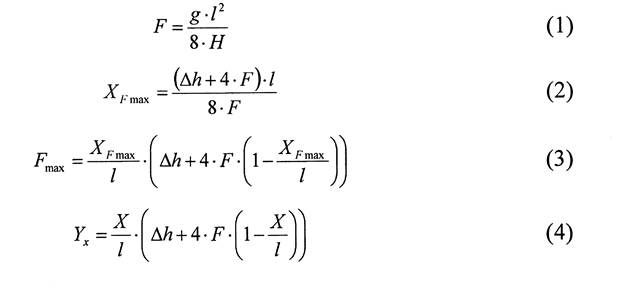Таблица 1