Исследование влияния температуры на натяжение и стрелы провеса проводов. Изучение состояния свободно подвешенного провода, страница 2

Х,м	1,7	1,8	1,9	2,0	2,1	2,2	2,3	2,4
расчётное	0,172	0,178	0,184	0,189	0,1935	0,198	0,2016	0,205
фактическое	0,166	0,172	0,178	0,183	0,187	0,191	0,1946	0,198
	0,006	0,006	0,006	0,006	0,0065	0,007	0,007	0,007

Х,м	2,5	2,6	2,7	2,8	2,9	3,0	3,1	3,2
расчётное	0,208	0,21	0,212	0,214	0,215	0,2156	0,2158	0,2154
фактическое	0,202	0,201	0,207	0,208	0,209	0,21	0,21	0,21
	0,006	0,005	0,005	0,006	0,006	0,0056	0,0058	0,0054

Х,м	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0
расчётное	0,215	0,2136	0,212	0,21	0,2075	0,2045	0,201	0,197
фактическое	0,209	0,208	0,207	0,206	0,204	0,2	0,196	0,192
	0,006	0,0056	0,005	0,004	0,0035	0,0045	0,005	0,005

Х,м	4,1	4,2	4,3	4,4	4,5	4,6	4,7	4,8
расчётное	0,192	0,190	0,183	0,177	0,171	0,1645	0,1575	0,15
фактическое	0,187	0,185	0,178	0,172	0,166	0,16	0,155	0,15
	0,005	0,005	0,005	0,005	0,005	0,0045	0,0025	0

а) Чем можно объяснить появление отклонений между фактическими и расчётными значениями?

Отклонения появились из-за неточности измерений и пренебрежением t при расчётах.

б) Как изменяется место положения нижней точки провода в пролёте при изменении натяжения провода?

Нижняя точка провода поднимется вверх по оси Y и сместится в сторону грузокомпенсации.

Лабораторная работа № 3.2.

Порядок выполнения работы № 3.2

2. Расчёт стрел провеса несущего троса и контактного провода при различных натяжениях несущего троса.

а) Задаётся натяжение несущего троса равное 1,5 даН, а контактному проводу равное 1 даН. При этом натяжении несущего троса по линейке определяется стрела провеса несущего троса и отметка положения контактного провода. Полученные данные заносятся в табл.2. Необходимо отметить, что при этом контактный провод расположен беспровесно.

б) С помощью грузов задаётся натяжение несущего троса равное 2даН, по линейке измеряется провес несущего троса в середине пролёта и отметка положения контактного провода при этом натяжении несущего троса (в середине пролёта).

Определяется провес контактного провода как разница между отметкой контактного провода при натяжении несущего троса равным 1,5 даН и при 2 даН. Полученные данные заносятся в табл.2.

в) Натяжение несущего троса принимаем равным 1 даН и проводим измерения аналогично вышеприведённому пункту.

г) Определяются стрелы провеса несущего троса и контактного провода по приведённым выше формулам. Рассчитываем разницу между полученным фактическим значением и расчётным.

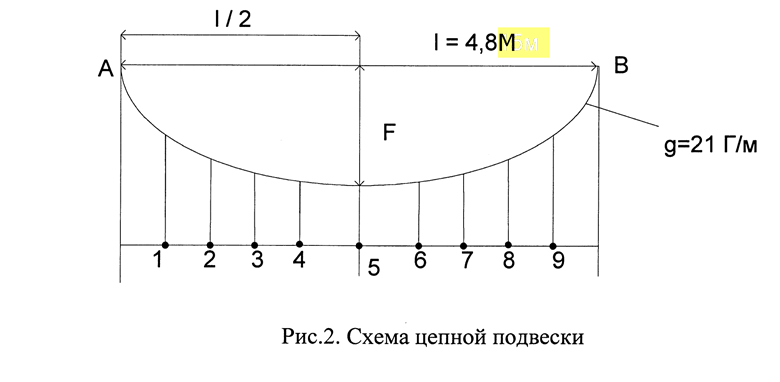
Gп=0,05514 даН/м; К=1,0 даН; l=4,8 м; Тх1=Т0=1,5даН; Тх2=2,0 даН; Тх=1,0 даН.

Рабочие формулы:

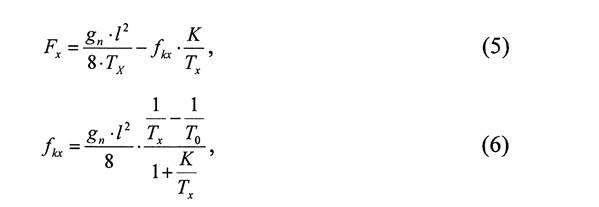
Таблица 2

Тx	Fхр	Fхф		fхр	fхф
1,5	0,106	0,115	0,009	0	0	0
2,0	0,88	0,95	0,07	-0,018	-0,02	0,002
1,0	0,132	0,140	0,008	0,026	0,025	0,001

а) Чем можно объяснить появление отклонений между фактическими и расчётными значениями?

Отклонения появились из-за неточности измерений и пренебрежением t при расчётах.

б) Почему при одинаковом изменении натяжения Т относительно Т0 на  0,5 даН провес F изменяется относительно Fо не на одинаковые значения?

Провес F изменяется относительно Fо не на одинаковые значения, потому что при большем грузе грузокомпенсации несущего троса часть нагрузки несущий трос берёт с контактного провода.

в) Чем отличается работа полукомпенсированной подвески от компенсированной?

При полукомпенсированной подвеске несущий трос жёстко зафиксирован, а в компенсированной подвеске несущий трос и контактный провод имеют грузокомпенсацию.

г) В чем преимущества компенсированной подвески по отношению к полукомпенсированной?

Компенсированная подвеска лучше реагирует на перепады температур, у неё меньше стрела провеса.