







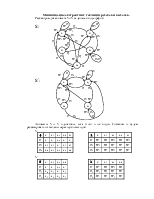









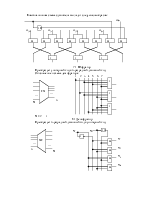


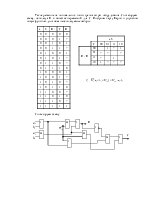


Соединение автоматов.
1.Параллельное соединение двух автоматов.
Пусть даны два автомата: S1 и S2 – с различными собственными внутренними, входными и выходными алфавитами, начальными состояниями функциями переходов и выходов.
Их параллельное соединение будет выглядеть следующим образом:
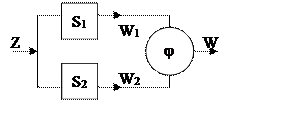 Согласно
схеме автоматы определяются так:
Согласно
схеме автоматы определяются так:
S1=(A1, Z, W1, d1, l1,a11)
S2=(A2, Z, W2, d2, l2,a12)
Проводя замену, «объединяя» автоматы получим новый автомат S, у которого:
· внутренний алфавит образуется из всевозможных пар состояний автоматов S1 и S2:
A = A1*A2.
· выходной алфавит есть функциональная зависимость j от W1 и W2:
W = j(W1, W2)
· новая функция переходов формируется зависимостью от d1, d2 и текущего элемента входного алфавита zf :
d(am, zf) = (d(am1, zf), d(am2, zf))
· новая функция выхода формируется в зависимости j от функций l1, l2 текущего элемента входного алфавита zf :
l(am, zf) = j(l1(am1, zf), l2(am2, zf))
ПРИМЕР:
Пусть имеется параллельное соединение автоматов S1 и S2:
 Автоматы
определяются двумя векторами:
Автоматы
определяются двумя векторами:
S1=(A, Z, W1, d1, l1,a1)
S2=(B, Z, W2, d2, l2,b1)
Таблицы переходов и выходов автомата S1:
d1: l1:
|
a1 |
a2 |
a3 |
|
|
Z1 |
a1 |
a1 |
a3 |
|
Z2 |
a3 |
a3 |
a2 |
|
a1 |
a2 |
a3 |
|
|
Z1 |
W11 |
W12 |
W12 |
|
Z2 |
W11 |
W11 |
W11 |
Таблицы переходов и выходов автомата S2:
d2: l2:
|
b1 |
b2 |
|||
|
Z1 |
b1 |
b2 |
||
|
Z2 |
b2 |
b1 |
||
|
b1 |
b2 |
|||
|
Z1 |
W21 |
W22 |
||
|
Z2 |
W22 |
W21 |
||
Таблица функции j:
j:
|
W21 |
W22 |
|
|
W11 |
W1 |
W2 |
|
W12 |
W2 |
W3 |
Так как внутренний алфавит определяется формулой: A = A1*A2, таблица переходов нового автомата будет выглядеть следующим образом:
d:
|
a1b1 |
a1b2 |
a2b1 |
a2b2 |
a3b1 |
a3b2 |
|
|
Z1 |
a1b1 |
a1b2 |
a1b1 |
a1b2 |
a3b1 |
a3b2 |
|
Z2 |
a3b2 |
a3b1 |
a3b2 |
a3b1 |
a2b2 |
a2b1 |
Составляется таблица следующим образом:
Теперь построим таблицу выходов нового автомата, руководствуясь следующими правилами:
l1:
|
a1b1 |
a1b2 |
a2b1 |
a2b2 |
a3b1 |
a3b2 |
|
|
Z1 |
W11W21 |
W11W22 |
W12W21 |
W12W22 |
W12W21 |
W12W22 |
|
Z2 |
W11W22 |
W11W21 |
W11W22 |
W11W21 |
W11W22 |
W11W21 |
Составим конечный вариант таблицы l, воспользовавшись таблицей выходов функции j:
· в соответствие каждым W1iW2j будем выбирать из таблицы j соответствующие значения W1k.
l:
|
a1b1 |
а1b2 |
a2b1 |
a2b2 |
a3b1 |
a3b2 |
|
|
Z1 |
W1 |
W2 |
W2 |
W3 |
W2 |
W3 |
|
Z2 |
W2 |
W1 |
W2 |
W1 |
W2 |
W1 |
Наш новый автомат S, замещающий S1 и S2 задан таблицами l и d.
2.Последовательное соединение двух автоматов.
3.
Пусть даны два автомата: S1 и S2 – с различными собственными внутренними, входными и выходными алфавитами, начальными состояниями функциями переходов и выходов.
Их последовательное соединение будет выглядеть следующим образом:
Согласно схеме автоматы определяются так:
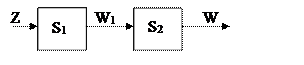 S1=(A1,
Z, W1, d1,
l1,a11)
S1=(A1,
Z, W1, d1,
l1,a11)
S2=(A2, W1, W, d2, l2,a12)
Проводя замену, «объединяя» автоматы получим новый автомат S, у которого:
· внутренний алфавит образуется из всевозможных пар состояний автоматов S1 и S2:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.