Связь между моделями автоматов Мили и Мура.
1.Переход от автомата Мура к автомату Мили.
Переход от модели Мура к модели Мили осуществляется просто. Так как в автомате Мили выходные сигналы W формируются вследствие перехода из одного состояния в другое под действием входных сигналов Z, то в модели Мили в соответствие каждому переходу мы будем ставить выходной сигнал W, соответствующий в автомате Мура выходному сигналу состояния, в которое мы переходим.
ПРИМЕР:
Пусть в
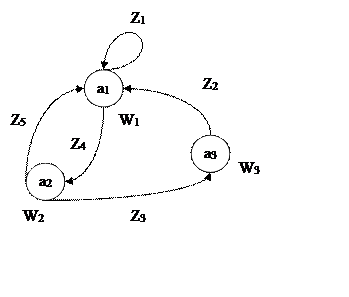
виде графа задан автомат Мура.
На этом ориентированном графе изображен автомат Мура: Имеется три состояния a1, a2, a3 каждому состоянию соответствует свой выходной сигнал W1, W2, W3. Между состояниями имеются связи по которым совершается переход из одного состояния в другое под действием входных сигналов Z1, Z2, Z3, Z4, Z5.
В соответствии с правилом получим автомат Мили:
 |
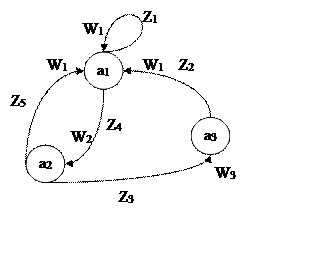Состоянию a1 Автомата Мура соответствует выходной сигнал W1. Отметим все переходы в состояние a1 выходными сигналами W1. В нашем случае это переходы под действием сигналов Z1, Z2, Z5,
Аналогично все переходы в состояние a2 отметим выходными сигналами W2, а все переходы в состояние a3 – W3.
2.Переход от автомата Мили к автомату Мура.
Этот переход осуществляется немного сложнее. Основное правило, которым надо руководствоваться при осуществлении данного перехода таково:
Вследствие того, что в автомате Мура каждому состоянию соответствует выходной сигнал, то: при переходе каждое состояние ai исходного автомата Мили порождает столько состояний автомата Мура, сколько различных выходных сигналов в автомате Мили вырабатывается при входе в это состояние.
ПРИМЕР:
Пусть в виде графа задан автомат Мили. Осуществим переход к автомату Мура, а затем вновь к автомату Мили.
 |
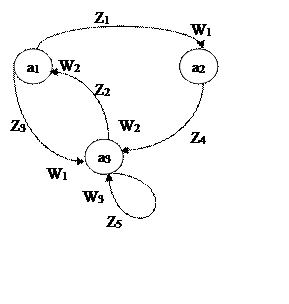На этом ориентированном графе изображен автомат Мура: Имеется три состояния a1, a2, a3 При переходах из состояния в состояние формируются выходные сигналы W1, W2, W3. Между состояниями имеются связи по которым совершается переход из одного состояния в другое под действием входных сигналов Z1, Z2, Z3, Z4, Z5.
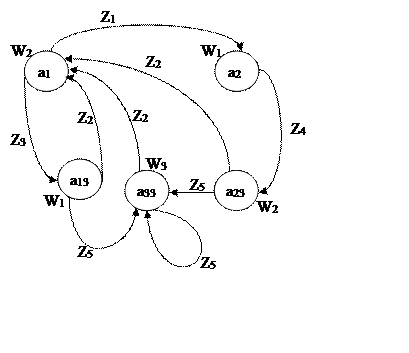
Перейдем к автомату Мура руководствуясь вышеописанным правилом:
При
входе в каждое из состояний a1 и a2
вырабатывается всего 1 входной сигнал W2 и W1 соответственно,
следовательно, они новых состояний не порождают.
При входе в состояние а3 вырабатываются три выходных сигнала W1, W2 и W3 при входных сигналах Z3, Z4 и Z5 соответственно, следовательно, это состояние порождает три состояния: a13, a23 и a33 соответственно.
Расставив связи и входные сигналы соответственно исходному автомату получим автомат изображенный левее.
Перейдем теперь по описанному в первом пункте правилу к автомату Мура.
 |
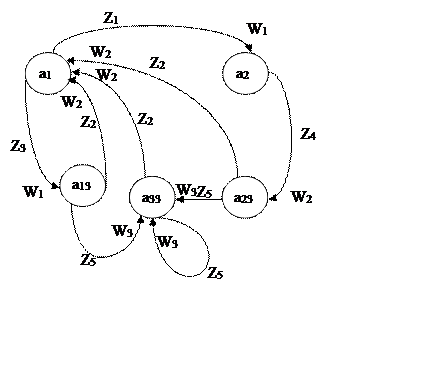Состоянию a1 Автомата Мура соответствует выходной сигнал W2. Отметим все переходы в состояние a1 выходными сигналами W2. В нашем случае это переходы под действием сигнала Z2.
Аналогично все переходы в состояние a2 отметим выходными сигналами W1, все переходы в состояние a13 – W1, все переходы в состояние a23 – W2, все переходы в состояние a33 – W3.
В итоге мы получим автомат изображенный левее.
Как видно, новый автомат Мили отличается от исходного. Эти два автомата одинаковы, просто, вследствие порожденных переходом к автомату Мура состояний, новый автомат получился не минимизированным.
Минимизация абстрактных таблиц переходов и выходов.
Рассмотрим два автомата S и S’ заданные в виде графов:
 |
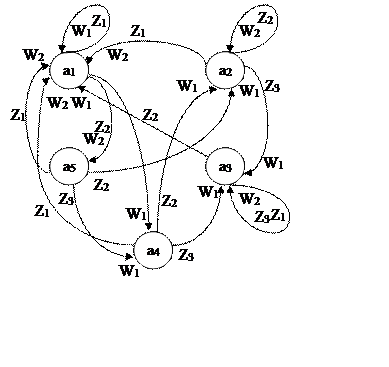S:
|
|||
 |
|||
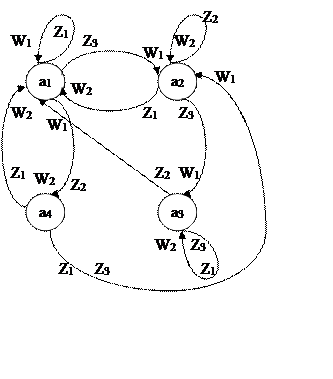S’:
Автоматы S и S’ одинаковы, хотя этого и не видно. Составим и будем рассматривать их таблицы переходов и выходов:
S:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.