Соединение автоматов. Параллельное соединение двух автоматов. Соединение двух автоматов с обратной связью, страница 7

Выделяют два алгоритма кодирования:

1.  Алгоритм кодирования для  D-триггеров.

При кодировании состояний исходят из того, что сложность схем формирования функции возбуждения находится в пропорциональной зависимости от количества единиц в коде состояний.

Поступают следующим образом:

1)  Каждому состоянию a_n ставиться в соответствие число N_m равное количеству переходов в это состояние.

2)  Упорядочивается последовательность N₁ N₂ … N_M по убыванию.

3)  Коду a_s у которого N_s=max{ N₁ N₂ … N_M} присваиваем значение K_as=00…0.

4)  Следующим кодом r разрядностью R присваиваются значения:

000…001

000…010

000…100

…………

001…000

010…000

100…000

Затем будем искать коды, содержащие большее число единиц. Чем чаще используется состояние, тем меньше в нем единиц.

2.  Эвристический алгоритм кодирования.

Этот алгоритм позволяет минимизировать суммарное число изменений состояний элементов памяти, что в большинстве случаев приводит к упрощению комбинационной схемы формирующей функции возбуждения. Он используется в автоматах синтезированных на базе RS, T, JK триггеров.

Алгоритм кодирования таков:

1)  На основе неориентированного графа переходов автомата с указанием веса ребер P (количество переходов между состояниями) строится матрица T составленная из всех пар номеров состояний между которыми имеется переход при этом номер 1-ого состояния пары должен быть меньше 2-ого.

2)  Указываются веса пар переходов P и вычисляются суммы весов компонентов пар. (Под весом компонента понимается число его появлений в матрице T).

3)  Строится матрица M за счет перестановки матрицы T в порядке убывания весов пар, при этом каждый раз выбирается пара с наибольшим весом среди тех пар, которые имеют общий компонент с теми парами, которые уже были внесены в список пар ранее. Данная процедура (п.3) продолжается, пока в матрицу M не будут внесены все пары. В случае равенства весов пар предпочтение отдается той паре, у которой больше сумма весов компонентов. Если и по этому показателю нельзя отдать предпочтение ни одной из пар, то в матрицу M включается первая из группы с одинаковыми показателями.

4)  Состояния из первой строки кодируется как 00…00 (K₁) и 00…01 (K₂)

5)  Переходим к матрице M^’ вычеркивая первую закодированную строку матрицы M.

6)  Обозначаем как a. Незакодированный элемент 1-ой строки матрицы M^’ и строим матрицу M₂, выбирая из M^’ строки содержащие a. Закодированные ранее кодами K_a элементы матрицы M_a образуют множество B_a.

7)  Для каждого K_ai (i= 1…F) ищется множество соседних неиспользованных кодов отличающихся в 1-ом разряде. В случае отсутствия соседних кодов отыскиваются коды отличные в 2-х разрядах и т.д.

8)  Каждый из найденных кодов проверяется на возможность кодирования им состояния a, при этом для каждого из вариантов кодирования считается величина , представляющая собой сумму произведений весов дуг P, связывающих кодируемое состояние a с уже закодированным, на кодовые расстояние d. (Количество несовпадающих разрядов). a кодируется по возможности кодом, которому соответствует минимальная величина W_g из матрицы M^’ вычеркивается. Строки в которых оба элемента закодированы и в случае наличия в ней незакодированных элементов осуществляется переход к пункту 6.

ПРИМЕР:

Задана таблица переходов автомата. Закодировать состояния по эвристическому алгоритму.

	a1	a2	a3	a4	a5
Z1	a3	a1	a2	a1	a3
Z2	a5	a3	a2	a2	a1
Z3	a2	a4	a1	a1	a4

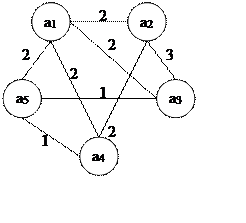
Построим неориентированный граф и обозначим веса: