ЛАБОРАТОРНО-ПРАКТИЧЕСКАЯ РАБОТА №3
«Исследование электрических схем трехфазного тока»
1. Цель работы:
1. Ознакомление с методикой построения схем и моделирования работы устройств в компьютерной лаборатории электротехники и электроники.
2. Исследование схем соединения электрических цепей переменного трехфазного тока.
2. Краткие теоретические сведения.
2.1. Трехфазные электродвижущие силы и их представление.
Трёхфазная система- это такая электрическая система где действуют три э.д.с. с одинаковой пульсацией, с одинаковым действующим значением, но сдвинутые по фазе друг от друга на 120° (Рис.1)
![]() ;
; ![]() ;
; ![]() .
.
В комплексной форме с действующими значениями получим:
![]() ;
; ![]() ;
; ![]() .
.
Основное соотношение для трёхфазной системы может быть записано, как в мгновенных значениях, так и в комплексном виде:
![]() ;
;
![]() .
.
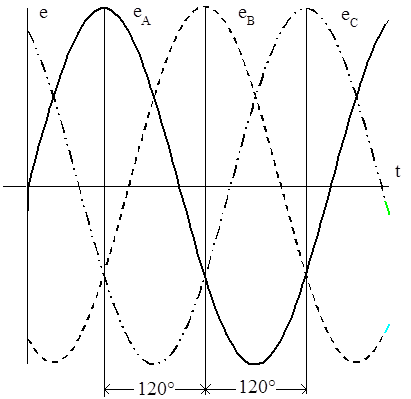
Рис. 1
На рисунке 2 представлена векторная диаграмма трёхфазной системы э.д.с. на комплексной плоскости.
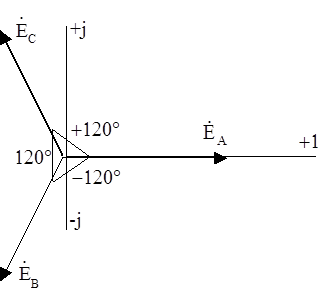
Рис.2
Фазы генератора в основном соединяются по схеме "звезда".
2.2. Соединение фаз генератора звездой.
Это соединение обмоток генератора, когда все их концы (X,Y,Z) соединены в одну точку, называемую нейтральной N (Рис.3).
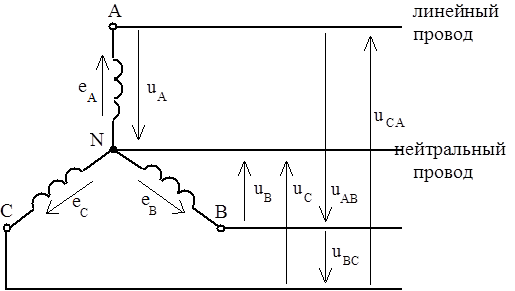
Рис.3
Напряжения между нейтральной точкой и каждой фазой называются фазными
![]() .
.
Напряжения между фазами называются линейными
![]() .
.
Согласно II закону Кирхгофа в комплексной форме имеем:
![]() ;
; ![]() ;
; ![]() .
.
Таким образом на комплексной плоскости можно построить векторную диаграмму напряжений трёхфазной системы (Рис.4)
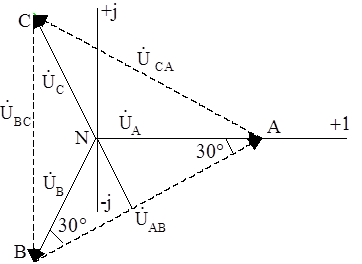
Рис.4
Из треугольника ANB
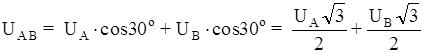 , так
как
, так
как ![]() и
и ![]() , то
получим соотношение между линейными и фазными напряжениями для трёхфазного
источника соединённого звездой
, то
получим соотношение между линейными и фазными напряжениями для трёхфазного
источника соединённого звездой
![]() .
.
2.3 Соединение нагрузки звездой.
2.3.1Симметричная нагрузка(Рис.5).
Нагрузка
называется симметричной, если ![]() , а также
равны их модули
, а также
равны их модули ![]() и
начальные фазы
и
начальные фазы ![]() .
.
Пренебрегая сопротивлением нейтрального и линейных проводов, можно констатировать, что
![]() ;
; ![]() ;
; ![]() , и
тогда токи будут
, и
тогда токи будут
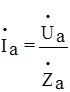 ;
; 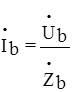 ;
; 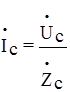 .
.
Согласно
I закону Кирхгофа: ![]() , однако
равны эффективные значения
, однако
равны эффективные значения ![]() и
начальные фазы
и
начальные фазы ![]() .
.
Таким образом, констатируем, что линейные и фазные токи равны
![]()
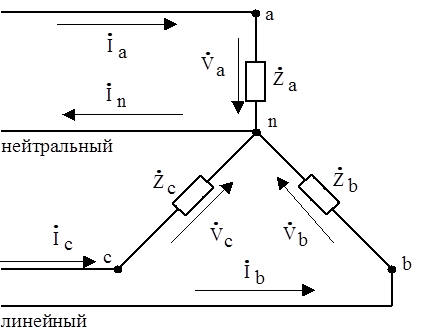
Рис 5
На комплексной плоскости три вектора тока образуют симметричную звезду (Рис.6) и тогда
![]() .
.
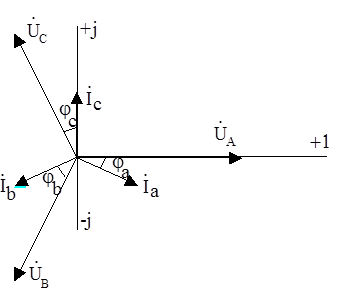
Рис.6
2.3.1.Несимметричная нагрузка(Рис.7).
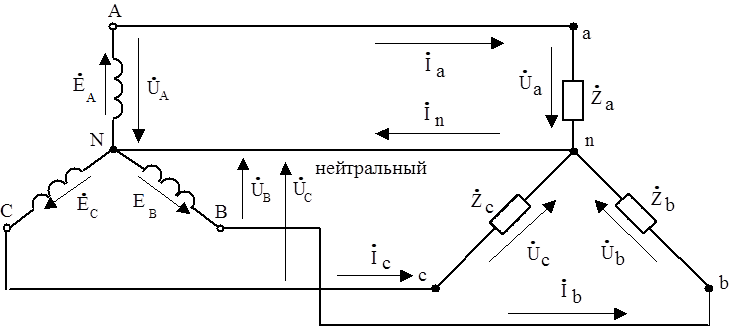
Рис.7
Нагрузка
называется несимметричной, если ![]() , тогда
токи
, тогда
токи ![]() и, как следствие, ток в
нейтральном проводе
и, как следствие, ток в
нейтральном проводе
![]()
будет не равен нулю.
Результат можно представить в виде векторной диаграммы (Рис.8).
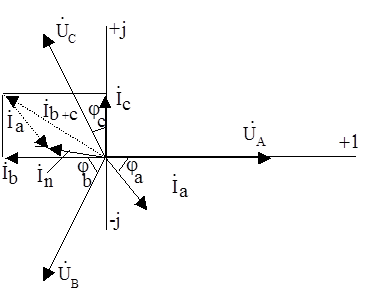
Рис.8
Если
нейтральный провод будет оборван, то ток ![]() ,
однако сумма токов
,
однако сумма токов ![]() и
поэтому появится напряжение
и
поэтому появится напряжение ![]() между
точками N и n.
между
точками N и n.
Это напряжение может быть рассчитано по формуле для двух узлов:
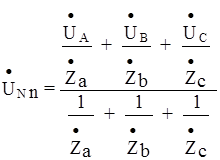 .
.
В этом случае трехфазная система становится несимметричной и напряжения на нагрузке для каждой фазы, фазные токи и ток в нейтральном проводе рассчитываются согласно формулам:
![]() ,
, ![]() ,
, ![]() .
.
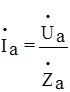 ;
; 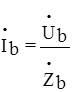 ;
; 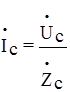 .
.
![]() .
.
На рисунке 9 представлены изменения в векторной диаграмме для этого случая. Фазные напряжения не одинаковы, однако фазные токи образуют симметричную звезду и их векторная сумма равна нулю.
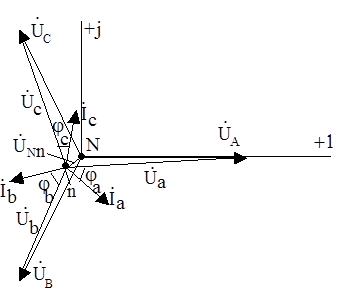
Рис.9
2.4. Соединение нагрузки треугольником (Рис.10).
2.4.1.Симметричная нагрузка.
Для
симметричной нагрузки ![]() , а также равны их
модули
, а также равны их
модули ![]() и начальные фазы
и начальные фазы ![]() .
.
Пренебрегая сопротивлением линейных проводов можно констатировать, что
![]() ;
; ![]() ;
; ![]() , и
тогда токи будут
, и
тогда токи будут
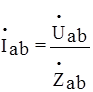 ;
; 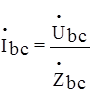 ;
; 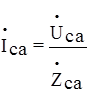 .
.
Согласно I закону Кирхгофа, в комплексной форме имеем:
![]() ;
; ![]() ;
; ![]() .
.
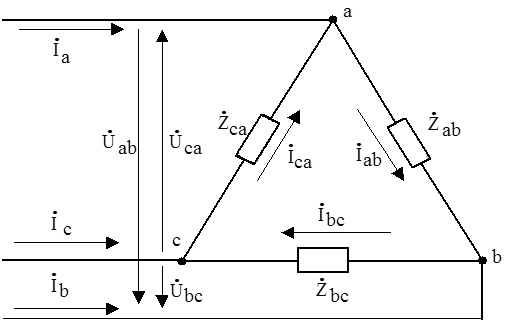
Рис.10
Диаграммы на комплексной плоскости иллюстрируют результат (Рис.11.а,в).
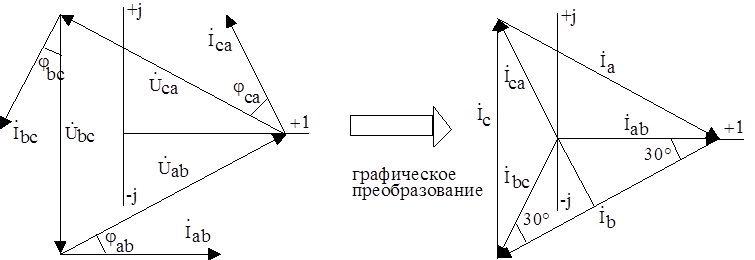
a) в)
Рис. 11
Согласно рисунку 11.в получим:
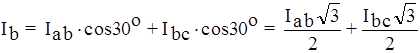 , так
как
, так
как ![]() и
и ![]() , то
получим соотношение между линейными и фазными токами для трёхфазной симметричной
нагрузки соединённой треугольником
, то
получим соотношение между линейными и фазными токами для трёхфазной симметричной
нагрузки соединённой треугольником
![]()
2.4.2. Несимметричная нагрузка.
В случае несимметричной нагрузки метод расчета одинаковый, однако, различия появляются при расчете токов и надо рассчитывать токи, используя I закон Кирхгофа. На рисунке 12 представлены изменения в векторной диаграмме.
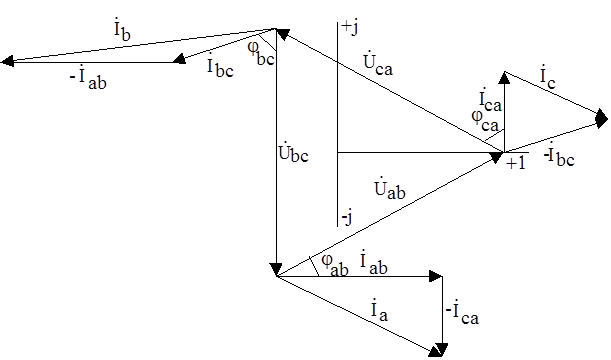
Рис.12
2.5. Мощность трехфазной цепи.
Трёхфазная мощность - это сумма фазных мощностей в мгновенных значениях:
![]() .
.
Для активных, реактивных и полных мощностей получаем следующие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.