|
№ |
T_noise |
U_noise_p |
U_noise_m |
|
2 |
|
|
|
Построим графики на выходе и входе ЛС для шума типа сигнала.
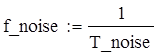
![]()
Определим образцовую функцию, заданного по варианту сигнала и построим один её период:
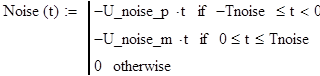
Зададим диапазон изменения времени:
![]()
Строим график «образцовой» функции:
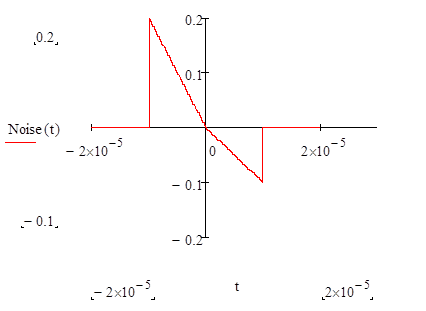
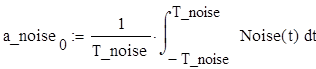
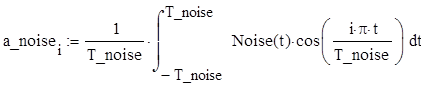
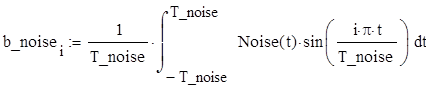
Запишем формулу для сигнала U_noise(t) и построим её график по 20 гармоникам:

Gmax: = 20 , i: = 0 .. 20
![]()
Переопределим диапазон изменения времени и построим график:
![]()
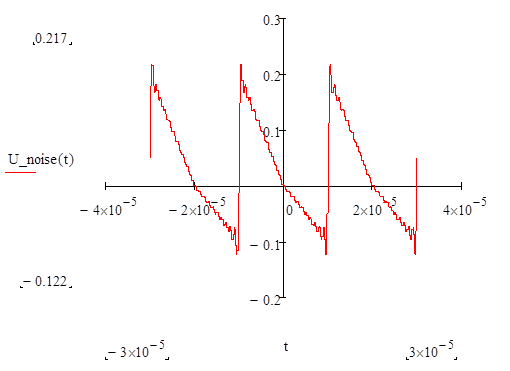
Действительный и мнимый спектры сигнала и шума имеют вид:
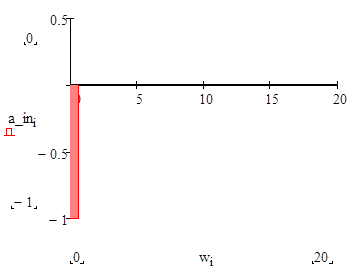
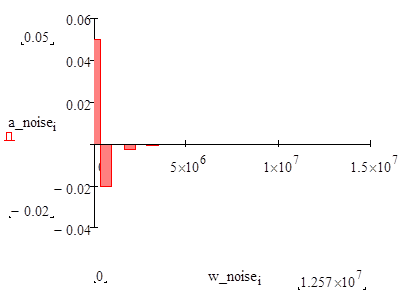
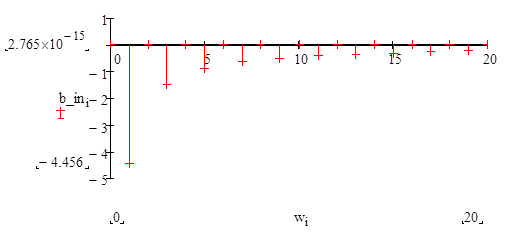
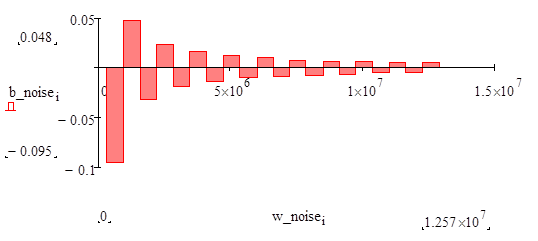
Как видим в сигнале отсутствует действительная, а в шуме мнимая часть спектра.
Мощность сигнала и шума составят:
![]() t1:= 0 ,
t1:= 0 ,
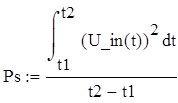 , Ps =12.252
, Ps =12.252
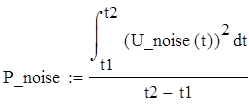 ,
, ![]()
Число гармоник, пропускаемых ЛС: K = 32.
Обычная (не круговая) частота - полоса пропускания ЛС в Гц:
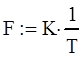
По формуле Найквиста пропускная способность составит:
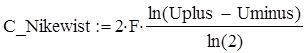 ,
, ![]()
По формуле Клода Шеннона пропускная способность составит:
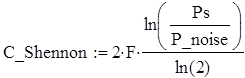
![]()
Вывод: при данной комбинации шума, производительность по Шеннону больше Найквиста в 3,876 раза. Если по Шеннону получили почти 7, то можно увеличить количество уровней сигнала. Пропускная способность будет равна при использовании 1887 уровней по Найквисту.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.