Дифракция света. Принцип Гюйгенса – Френеля. Построение кольцевых зон

Рассмотрим случай прохождения света через круглое отверстие. Пусть , рис. 3, точечный источник света, -  круглое

Рис. 3 Построение кольцевых зон

отверстие в непрозрачном экране, лежащее от на расстоянии . Это отверстие пропустит лишь часть сферической волны, исходящей из . Определим действие этой волны в точке , лежащей на пря Рис. 4 К подсчету размеров кольцевых зон мой , которая проходит через центр отверстия , на расстоянии  от от верстия. Для этого разделим волновую по -

верхность на кольцевые зоны – зоны Френеля, построенные таким образом, чтобы расстояния от краев соседних зон до точки  разнились на половину длины волны:

            (1)

Тогда колебания, приходящие в точку  от соответствующих частей соседних зон, будут иметь разность хода  , т. е. придут в точку  в противоположных  фазах.

Амплитуда колебаний, приходящих от отдельной зоны, зависит от площади этой зоны, от расстояния от зоны до точки  и от угла наклона между   и нормалью к поверхности зоны. Покажем прежде всего, что площади зон примерно одинаковы. Обозначим через - радиус - зоны. Из рис. 4 имеем

                           (2)

откуда

                                                    (3)

Но по (1) расстояние до - й зоны  на  больше расстояния :

;

осюда

                                               (4)

из (4), считая, что длина волны много меньше расстояния , приближенно получим

                                                          (5)

после чего равенство (3) примет вид

                                                       (6)

Площадь поверхности сферического сегмента радиуса равна

, подставляя сюда (6), получим

                                              (7)

В пределах этого сегмента уменьшается - кольцевых зон откуда площадь одной зоны  может быть представлена как разность площади этого сегмента и сегмента, охватывающего - зону:

откуда

                                                     (8)

Таким образом, площадь зоны в указанном приближении не зависит от ее номера , т. е. площади всех зон приблизительно одинаковы. Следовательно, амплитуды колебаний, доходящих от отдельных зон до точки , зависят лишь от расстояния  и угла, который направление  составляет с нормалью к поверхности зоны. С увеличением номера зоны  расстояние  возрастает и возрастает угол наклона, поэтому амплитуды колебаний, доходящих  до точки  от отдельных зон, должны монотонно убывать с увеличением номера зоны :

Так как фазы колебаний, приходящих в точку  от двух соседних зон, противоположны, то амплитуда суммарного колебания, вызванного действием  зон, равна

                 (9)

где знак последнего члена  положителен при нечетном   и отрицателен при четном .

Очевидно, что при четном числе зон их действия попарно ослабляют друг друга и амплитуда суммарного колебания в точке  незначительна; При нечетном числе зон действие одной из зон остается не ослабленным и амплитуда больше, чем при четном числе зон. Более точное значение мы получим, разбив в сумме (9) все нечетные члены на два слагаемых:

, ;

Тогда при нечетном  получим

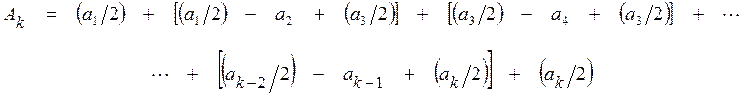(10)

а при четном  имеем

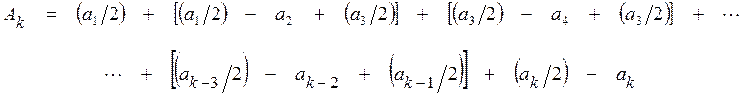(11)

Так как, по сказанному выше, амплитуда монотонно убывают с возрастанием номера , то приближенно можно положить амплитуду, вызванных какой – либо  - й зоной, равной полу сумме амплитуд колебаний, вызванных  - й и  - й зонами:

, поэтому все слагаемые в рядах (10) и (11), выделенные скобками, равны нулю и, следовательно, при нечетном :

,                                                (12)

а при четном :

                               (13)

Если число зон  достаточно велико, то амплитуды колебаний, вызванных соседними  и  зонами, мало отличаются друг от друга, откуда приближенно

.

Таким образом, равенства (12) и (13) принимают вид:

                                                 (15)

где знак  “”, а знак “ - ” соответствует четному числу зон.

По формуле (2) радиус  - й зоны определяется равенством

Полагая, пренебрежем , тогда

, подставляя сюда вместо  его значение по (6), получим

, наконец, заменяя , по (5), через , найдем

, откуда

                                                        (16)

Отметим, что  одновременно есть радиус рассматриваемого отверстия в экране. Отсюда получаем, что отверстие радиуса  открывает часть волнового фронта, на котором умещается число зон

                                            (17)

Для плоского фронта волны, падающего на экран , формула (17) принимает вид:

              (18)

или

                                                          (19)

где - угол, под которым видно отверстие в экране из точки , рис. 4.

Амплитуда суммарного колебания в точке  зависит от числа открытых зон . Для заданных: - длины волны,  - радиуса отверстия в нем и места положения экрана -  число открытых зон  будет различным.

В тех точках , для которых  нечетно, амплитуда суммарного колебания  больше, а  в тех точках , для которых  четно, она меньше. Квадрат амплитуды определит энергию колебаний. В свою очередь энергия световых колебаний определяет освещенность. Таким образом, при продвижении вдоль прямой , рис. 3, мы будем встречать то большие, то меньшие освещенности.

При данных же  и , т. е. при данном расположении источника света, экрана с отверстием и точки наблюдения будет зависеть от размеров отверстия  и его отношения к длине волны, (18), (19).

Таким образом, мы приходим к выводу: свет не распространяется прямолинейно, освещенность в точке  определится  размером и положением отверстия , она определяется действием всех точек, лежащих на открытой части волнового фронта.

Если размеры отверстия увеличить до бесконечности, т. е. оставить открытой или не закрывать всю поверхность волнового фронта