Электромагнитные волны. Волновое уравнение. Напряженность электрического поля в электромагнитной волне

Лекция № 2

Электромагнитные волны

1.  Волновое уравнение

Предположим, что некоторая физическая величина  распространяется в направлении со скоростью . В случае электромагнитных волн под  можно подразумевать напряженность электрического или магнитного поля.

Видим [см. Л№1_О_05, (8) и (9)], что общая форма записи этого процесса есть

                                                           (1)

где обозначает время, - координату рассматриваемой волны, а - символ произволь ной функции.

Таким образом, любая произвольная функция, если она зависит от аргумента , выражает волнообразный процесс.

Чтобы убедиться в этом, предположим, что наблюдатель движется в положитель ном направлении оси со скоростью .

Подобным же образом можно убедиться, что соотношение

                                                           (2)

выражает то обстоятельство, что величина  распространяется в отрицательном направлении оси .

Если в (1) и (2) , то в общем случае

.

Это выражение представляет распределение  в момент времени . Если  - напряженность электрического поля в электромагнитной волне, то последняя формула выражает распределение поля в пространстве в начальный момент времени. Следовательно, вид функции  зависит от начальных условий процесса. В частности, если  обозначает синусоидальный  или косинусоидальный процессы, то (1) переходит в уравнение гармонической волны[см. Л№1_О_05, (8)]. Таким образом (1) или (2) представляют собой общее выражение волны, распространяющейся вдоль оси .

Функция  удовлетворяет простому дифференциальному уравнению. Чтобы найти его продифференцируем (1) и (2) два раза по координате:

, где штрихами обозначено дифференцирование по всему аргументу . Вторая же частная производная по времени равна

здесь точками обозначено дифференцирование по времени.

Сравнивая эти выражения, мы видим, что искомое дифференциальное уравнение есть

                                                  (3)

Оно называется волновым уравнением.

Если волна распространяется во всех направлениях, то волновое уравнение имеет вид

              (4)

Таким образом, если какая – либо физическая величина распространяется волнообразно, то она удовлетворяет волновому уравнению. И обратно, если удается показать, что рас сматриваемая величина подчиняется волновому уравнению, то можно утверждать, что возможно ее распространение в виде волны. При этом непосредственно получается и скорость распространения волны, которая равна квадратному корню из коэффициента при , где - оператор Лапласа.

2.  Плоские электромагнитные волны

Обратимся теперь к уравнениям Максвелла в дифференциальной форме:

a)  первая группа уравнений Максвелла

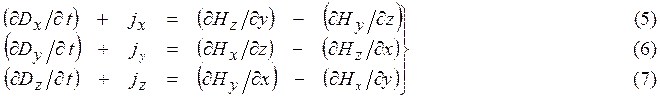
b) вторая группа уравнений Максвелла

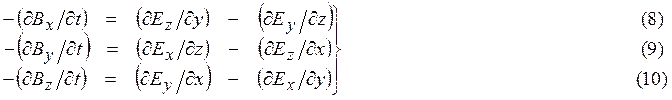
c) третье уравнение Максвелла в интерпретации Пуассона

                                               (11)

d) четвертое уравнение Максвелла

                                                 (12)

где  - компоненты вектора  - электрического смещения;  - компоненты вектора - напряженности магнитного поля, - компоненты вектора - индукции магнитного поля,  - компоненты вектора - напряжен ности электрического или электростатического поля;  компоненты вектора - плотности электрического тока; - объемная плотность заряда.

Наконец, следует напомнить, что различные величины, входящие в эти уравнения, не не зависимы (т. е. зависимы) и между ними существуют следующие связи:

                                                                       (13)

где - относительная магнитная проницаемость, - магнитная постоянная

                                                                  (14)

здесь - относительная диэлектрическая проницаемость вещества, - электрическая постоянная;

Сила же тока проводимости определяется плотностью тока , которая связана с напряженностью  законом Ома

                                                                             (15)

где - удельная электрическая проводимость вещества.

Будем считать, что среда представляет собой однородный диэлектрик. Тогда в уравнениях  (5)(7) и (15) нужно положить .