Лекция № 6
Поляризация света
1. Определение поляризации
Для продольных волн все направления, перпендикулярные линии распространения волн эквивалентны.
Для поперечных волн - они не эквивалентны.
Электромагнитные волны являются
поперечными, и их свойства зависят от ориентировки векторов ![]() и
и ![]() , характеризуемой
понятием поляризации.
, характеризуемой
понятием поляризации.
Если в процессе распространения
волн вектор ![]() лежит в одной и
той же плоскости, параллельной направлению распространения волн, то волны
называются линейно поляризованными; [(рис. 1), Л№2], рис. 1.
лежит в одной и
той же плоскости, параллельной направлению распространения волн, то волны
называются линейно поляризованными; [(рис. 1), Л№2], рис. 1.
Плоскостью поляризации называется
плоскость, в которой лежат векторы: ![]() и
и
![]() - волновой
вектор; подчеркнем, что
- волновой
вектор; подчеркнем, что ![]() -
это вектор индукции магнитного поля, а не электрический вектор
-
это вектор индукции магнитного поля, а не электрический вектор ![]() . Однако это
понятии такое понятие сейчас употребляется редко. Чаще говорят о плоскости
колебаний вектора
. Однако это
понятии такое понятие сейчас употребляется редко. Чаще говорят о плоскости
колебаний вектора ![]() .
.
2. Суперпозиция линейно поляризованных волн
Рассмотрим
суперпозицию двух линейно поляризованных волн одной и той же частоты,
распространяющихся в одном направлении. Для определенности будем считать, что
колебания ![]() первой волны
лежат в плоскости
первой волны
лежат в плоскости ![]() , а
второй – в плоскости
, а
второй – в плоскости ![]() , рис.
2. Тогда можно записать:
, рис.
2. Тогда можно записать:
![]() (1)
(1)
![]() (2)
(2)
здесь ![]() - сдвиг фаз
между колебаниями.
- сдвиг фаз
между колебаниями.
|
|
|
|
Рис. 1 Изменение векторов плоской волны в пространстве |
Рис. 2 Суперпозиция линейно поляризованных волн, приводящая к эллиптической поляризации |
Рассмотрим
напряженность ![]() электрического
поля суммарной волны в плоскости, перпендикулярной
направлению распространения волн при фиксированном значении
электрического
поля суммарной волны в плоскости, перпендикулярной
направлению распространения волн при фиксированном значении ![]() . С течением
времени конец вектора
. С течением
времени конец вектора ![]() описывает
в плоскости
описывает
в плоскости ![]() некоторую
замкнутую кривую. Найдем уравнение этой кривой. Перепишем (2) в виде
некоторую
замкнутую кривую. Найдем уравнение этой кривой. Перепишем (2) в виде
![]()
и с помощью (1) исключим из этого равенства ![]() и
и ![]() :
:
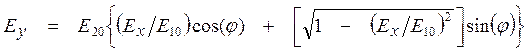 (3)
(3)
где ![]() и
и
![]() - амплитуды,
которые предполагаются положительными числами.
- амплитуды,
которые предполагаются положительными числами.
Перенося первое слагаемое в правой части (3)
на левую сторону, возводя обе части в квадрат, затем, деля на ![]() , после
перегруппировки членов приводим уравнение (3) к виду
, после
перегруппировки членов приводим уравнение (3) к виду
![]() (4)
(4)
Рассмотрим различные случаи, описываемые этим уравнением.
3. Эллиптическая и круговая поляризации
|
|
|
|
Рис. 3 Эллиптическая поляризация в частном случае,
когда главные оси эллипса коллинеарны направлениям колебаний |
Рис. 4 Эллиптическая поляризация в общем случае |
Если ![]() в (4) равен
нулю, а
в (4) равен
нулю, а ![]() , то (4)
принимает вид:
, то (4)
принимает вид:
![]() (5)
(5)
При ![]() это
выражение является уравнением эллипса с центром в начале координат и осями,
направленными воль осей системы координат. Полуоси эллипса, рис. 3, равны
это
выражение является уравнением эллипса с центром в начале координат и осями,
направленными воль осей системы координат. Полуоси эллипса, рис. 3, равны ![]() (по оси
(по оси ![]() ) и
) и ![]() (по оси
(по оси ![]() ).
).
Условие ![]() соблюдается при
соблюдается при
![]() (6)
(6)
тогда уравнения (1) и (2) принимают такой вид ![]()
![]() (7)
(7)
![]() (8)
(8)
Видно, что конец вектора ![]() вращается по
часовой стрелке при нечетном
вращается по
часовой стрелке при нечетном ![]() и
против часовой стрелки – при четном
и
против часовой стрелки – при четном ![]() .
.
В первом случае, т. е. когда ![]() - нечетное,
говорят о правой эллиптически поляри зованной волне, а во втором, т. е. при
- нечетное,
говорят о правой эллиптически поляри зованной волне, а во втором, т. е. при ![]() - четном – о
левой эллиптически поляризованной волне. Отметим, что наблюдение за вращением
вектора
- четном – о
левой эллиптически поляризованной волне. Отметим, что наблюдение за вращением
вектора ![]() ведется со
стороны, в которую движется волна (ось
ведется со
стороны, в которую движется волна (ось ![]() на рис. 3
направлена к нам).
на рис. 3
направлена к нам).
При ![]() эллипс становится
окружностью. Соответствующая волна называется поляризованной по кругу или
волной с циркулярной поляризацией.
эллипс становится
окружностью. Соответствующая волна называется поляризованной по кругу или
волной с циркулярной поляризацией.
Как и в случае волн с эллиптической поляризацией, могут быть волны с левой и правой циркулярной поляризацией.
Как и в случае волн с эллиптической поляризацией, могут быть волны с левой и правой циркулярной поляризацией.
При ![]() уравнение (4)
также описывает эллипс, однако его главные оси не совпадают с осями координат.
Как видно из (1) и (2), максимальные и минимальные значения составляющих
уравнение (4)
также описывает эллипс, однако его главные оси не совпадают с осями координат.
Как видно из (1) и (2), максимальные и минимальные значения составляющих ![]() и
и ![]() равны
равны ![]() и
и ![]() , поэтому эллипс
вписан в прямоугольник со сторонами
, поэтому эллипс
вписан в прямоугольник со сторонами ![]() и
и
![]() с центром в
начале координат, рис. 4. Ориентация эллипса и его параметры зависят от
с центром в
начале координат, рис. 4. Ориентация эллипса и его параметры зависят от ![]() . В частности,
следует обратить внимание, что для
. В частности,
следует обратить внимание, что для ![]() получается
эллиптически поляризованная волна даже при
получается
эллиптически поляризованная волна даже при ![]() . Направление
вращения суммарного вектора
. Направление
вращения суммарного вектора ![]() определяется
значением
определяется
значением ![]() .
.
4. Изменение вектора напряженности в пространстве при эллиптической и круговой поляризациях
|
|
Для фиксированного момента времени множество
точек, образуемых концом вектора Представлять себе эллиптически поляризо ванную волну можно так: на поверхности прямого эллиптического цилиндра прове дена винтовая линия, начало вектора |
|
Рис. 5 Изменение вектора |
5. Вырожденный случай эллиптической поляризации
При ![]() ,
, ![]() соотношение (4)
становится равенством
соотношение (4)
становится равенством
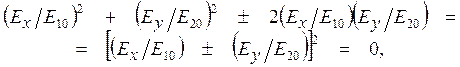
из которого при ![]() и
и ![]() находим прямые
находим прямые
![]() (9)
(9)
![]() (10)
(10)
Конец суммарного вектора ![]() движется по
соответствующей прямой, рис. 6 и рис. 7. Получается линейно поляризованная
волна, которая является предельным случаем эллиптически поляризованной волны,
рис. 4, при равенстве нулю одной из полуосей эллипса. При
движется по
соответствующей прямой, рис. 6 и рис. 7. Получается линейно поляризованная
волна, которая является предельным случаем эллиптически поляризованной волны,
рис. 4, при равенстве нулю одной из полуосей эллипса. При ![]() суммарное
колебание вектора
суммарное
колебание вектора ![]() происходит
в первом и третьем
происходит
в первом и третьем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.