Интерференция света. Когерентность монохроматичность волн и колебаний. Гармоническое колебание. Средний квадрат амплитуды результирующего колебания за промежуток времени

Лекция № 3

Интерференция света

1. Когерентность монохроматичность волн и колебаний

При сложении двух гармонических колебаний одного периода

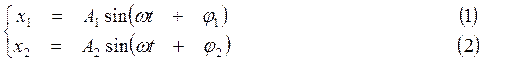
происходящих по одному направлению, получится вновь гармоническое колебание того же периода.

                                       (3)

амплитуда  и фаза которого определяется из следующих соотношений:

                          (4)

                  (5)

Формула (4) показывает, что квадрат амплитуды результирующего колебания не равен сумме квадратов амплитуд складывающихся колебаний, т. е. энергия результирующего колебания не равна сумме энергий складывающихся колебаний. Результат сложения зависит от разности фаз  исходных колебаний и может иметь любое значение в пределах : от , если   до , если .

Однако мы никогда не имеем дела со строго гармоническими колебаниями (1), (2), т. е. колебаниями длящимися бесконечно долго с неизменной амплитудой. Обычно колебания время от времени обрываются и возникают вновь уже с иной, нерегулярно измененной фазой, т. е. не являются строго гармоническими. В таком случае и результирующая интенсивность, если , также меняется с течением времени.

Мы не сможем следить за всеми изменениями если  и будем регистрировать только среднее во времени значение величины интенсивности , обозначаемое .

вводя обозначение , вычислим средний квадрат амплитуды результирующего колебания за промежуток времени , длящийся дольше, чем время нерегулярных изменений фазы :

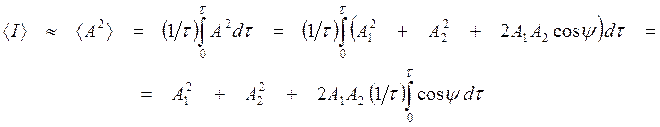            (6)

Если  остается неизменным в течение времени наблюдения , то

;

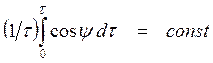следовательно

, т. е.

                                                                 (7)

При случайном же обрыве и возобновлении колебаний разность фаз изменяется совершенно беспорядочно, многократно пробегая за время  все значения от нуля до . Поэтому

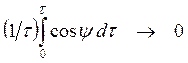, и мы имеем

, т. е.

                                                                                                                                                    (8)

Итак, при сложении двух колебаний одного периода надо различать два случая:

1)       разность фаз колебаний  сохраняется  неизменной за время ,

достаточное для наблюдений. Средняя энергия результирующего колебания отличается от суммы средних энергий исходных колебаний, (7), и может быть больше или меньше нее в зависимости от разности фаз. В этом случае, определяемом (7), колебания называются когерентными;

2)  сложение колебаний, когда разность фаз колебаний беспорядочно меняется за время наблюдения, приводит к тому, что средняя энергия результирующего колебания равна сумме средних энергий исходных колебаний; колебания в этом случае называются некогерентными и при их суммировании всегда наблюдается сложение интенсивностей, т. е. интерференция не имеет места.

Строго гармонические колебания одинаковой частоты всегда  когерентны между собой, т. к. они длятся не обрываясь, и имеющаяся у них разность фаз сохраняется без изменения сколь угодно долгое время.

Вопросы о монохроматичности колебаний в волнах обсуждались в [Л. № 2, (21) (23); (24)  (29)].

2.         Длина и время когерентности

Часть последовательности колебаний, на протяжении которой сохраняется их регулярность, называется цугом волн или волновым цугом.

Время испускания цуга волн называется длительностью цуга или временем когерентности. Пространственная протяженность цуга - длина цуга волн и время когерентности связаны очевидным соотношением

                                                                 (9)

где - скорость света.

Длина цуга волн и длина когерентности совпадают. Действительно, если разность хода интерферирующих пучков становится больше длины цуга волн, то в данной точке интерференционного поля складываются волны, испущенные атомом в момент времени, отличающиеся более чем на время когерентности. Но такие колебания не могут интерферировать. Следовательно, интерференция не может наблюдаться, если разность хода больше длины цуга, а максимальная разность хода при которой интерференция еще наблюдается, т. е. длина когерентности, равна длине цуга.

Используя связь между длиной когерентности и шириной спектрального интервала , можно найти соотношение между  и временем когерентности

, откуда, учитывая, что

, получаем

                                                                           (10)

где - ширина спектрального интервала в шкале частот.

Порядок интерференции связан с разностью хода интерферирующих световых пучков  и длиной волны соотношением

.

При интерференции немонохроматического света следует считать