Одноканальная двухфазная система массового обслуживания с отказами с разной производительностью приборов

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ»

филиал в г. Сергиев Посад

Кафедра ИТ-4

Отчет по лабораторной работе №5

по дисциплине «Моделирование»

Преподаватель: 

Студента:

спец. 230101

курс-4

группа ИТ4-06-01Д

Оценка

Подпись руководителя             ФИО руководителя

Сергиев Посад 2009 г.

Вариант №3.

Выполнение работы.

Система с отказами.

Имеется одноканальная двухфазная система массового обслуживания с отказами с разной производительностью приборов (рис. 1).

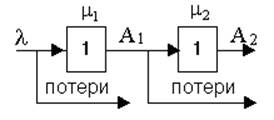
Рисунок 1 – Структурная схема системы с отказами

Обозначим состояния системы:

S₀₀ – первый и второй приборы свободны от обслуживания;

S₁₀ – первый прибор занят обслуживанием, второй свободен;

S₀₁ – первый прибор свободен, второй занят обслуживанием;

S₁₁ – оба прибора заняты обслуживанием.

Граф переходов системы показан на рис. 2.

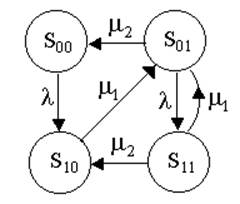Система дифференциальных уравнений:

Система линейных алгебраических уравнений:

Замечаем, неизвестных 3, а уравнений 4, следовательно, одно уравнение можно исключить. Последнее нормировочное уравнение исключать нельзя, поэтому исключим второе уравнение, как наиболее сложное. Запишем систему уравнений в упорядоченном виде

0 + 

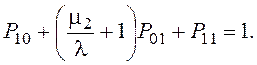
Аналитические расчеты.

Решение будем искать по правилу Крамера (через определители)

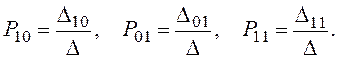
Здесь  определитель системы

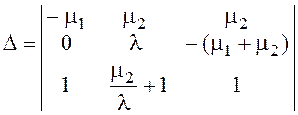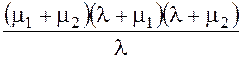 = – = -131,516

    определитель для P₁₀

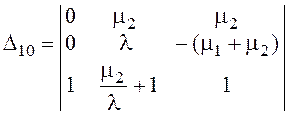 =  = -34,92

    определитель для P₀₁

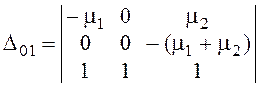 =  = -31,57

    определитель для P₁₁

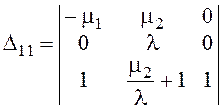 =  = -8.2

Таким образом, получаем

§  Вероятность того, что занят обслуживанием только первый прибор

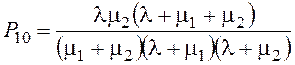 = 0,266

§  Вероятность того, что занят обслуживанием только второй прибор

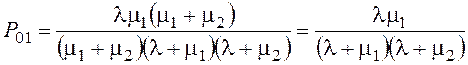 = 0,240

§  Вероятность того, что заняты оба прибора

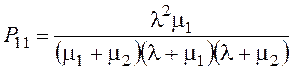 = 0,062

§  Вероятность того, что все приборы свободны от обслуживания, найдем из уравнения (1)

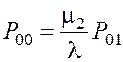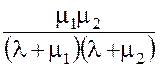=  = 0,432

Определим относительную и абсолютную пропускные способности системы.

Первый прибор отказывает заявке в обслуживании, если он занят обслуживанием другой заявки, а занят он в состояниях S₁₀ и S₁₁, поэтому

q₁ = 1 – (P₁₀ + P₁₁) = 0,672

§  Абсолютная пропускная способность первого прибора равна

A₁ =  = 1,344

§  Абсолютная пропускная способность первого прибора есть интенсивность потока заявок, поступающих на второй прибор.

Второй прибор занят в состояниях S₀₁ и S₁₁, поэтому

q₂ = 1 – (P₀₁ + P₁₁) = 0,698

§  Абсолютная пропускная способность второго прибора и системы в целом равна

A₂ = A₁q₂ = q₁q₂ = (1 –P₁₀ – P₁₁)(1 – P₀₁ – P₁₁) = 0,938

Программа.

lambda    equ  2

mu_1      equ  4.1

mu_2      equ  3.6

*

tab_T_syst          table m1,0,2,15; Таблица интервалов времени

*                                    нахождения заявок в системе

*

                    generate (exponential(1,0,(1./lambda)))

*

                    TEST E (F1&F2),1,MET1

                    SAVEVALUE 3+,1; Заняты обе фазы

MET1      TEST E (~F1&~F2),1,MET2

                    SAVEVALUE 10+,1; Обе фазы свободны

MET2      TEST E (F1&~F2),1,MET3;

                    SAVEVALUE 1+,1; Занята первая фаза, вторая свободна

MET3      TEST E (F2&~F1),1,MET4

                    SAVEVALUE 2+,1; Занята вторая фаза, первая свободна

MET4      TEST E (F1),1,MET5

                    SAVEVALUE 11+,1; занята первая

                    TERMINATE; потери 1

*

MET5      seize 1; Начало обработки заявки в первой фазе

          advance (Exponential(3,0,(1./mu_1)))

          release 1; Завершение обработки заявки в первой фазе

*

          TEST E (F2),1,MET6

                    SAVEVALUE 12+,1; занята вторая

                    TERMINATE; потери 2

*

MET6      seize  2; Начало обработки заявки во второй фазе

          advance  (exponential(3,0,(1./mu_2)))

          release  2; Завершение обработки заявки во второй фазе

*

                    tabulate  tab_T_syst

                    terminate  ; Удаление обслуженных заявок

* 

*         Задание времени моделирования

                    GENERATE 100000

*         Определение характеристик системы

          SAVEVALUE  P_00,(x10/n1);

          SAVEVALUE  P_10,(x1/n1)

          SAVEVALUE  P_01,(x2/n1)

          SAVEVALUE  P_11,(x3/n1)

          SAVEVALUE  P_sum,(x$P_00+x$P_01+x$P_10+x$P_11);

          SAVEVALUE  P_otk1,(x11/n1)

          SAVEVALUE  P_otk2,(x12/n1)

          SAVEVALUE  P_sum,(x$P_00+x$P_01+x$P_10+x$P_11);  

          SAVEVALUE Q_1 (1-(x$P_10+x$P_11))