Одноканальная двухфазная система массового обслуживания с отказами с разной производительностью приборов, страница 8

 7                        0     138611.000                           

 10                       0      45897.000                           

 13                       0      43347.000                           

 14                       0      56182.000                           

 15                       0      24051.000                           

 16                       0      27183.000                           

 17                       0      12427.000                           

 18                       0       3259.000                           

 P_00                     0          0.231                           

 P_1                      0          0.269                           

 P_2                      0          0.218                            

 P_3                      0          0.282                           

 P_SUM                    0          1.000                           

 P_10                     0          0.513                           

 P_20                     0          0.448                           

 P_11                     0          0.250                           

 P_21                     0          0.248                           

 P_12                     0          0.121                            

 P_22                     0          0.137                           

 P_1_1                    0          0.062                           

 P_2_2                    0          0.016                           

 P_O1                     0          0.763                           

 P_O2                     0          0.696                           

FEC XN   PRI         BDT      ASSEM  CURRENT  NEXT  PARAMETER    VALUE

199044    0      100000.582   199044      0      1

199045    0      200000.000   199045      0     42

Из отчета мы видим, что сумма вероятностей равна 1 и расчеты полученные в ходе моделирования совпадают с аналитическими расчетами, следовательно система смоделирована правильно.

Все полученные путём моделирования характеристики занесём в таблицу и сравним с данными аналитических расчётов:

Характеристика системы	Данные аналитических расчётов	Данные моделирования	Величина отклонения от данных аналитических расчётов, %
P1	0.488	0.488	0
P2	0.556	0.550	1
P00	0,227	0.231	1.7
P1	0.271	0.269	0.7
P2	0.217	0.218	0.46
P3	0.285	0.282	1
P10	0.512	0.513	0.2
P20	0.444	0.448	0.9
P11	0.25	0.250	0
P21	0,247	0.248	0.4
P12	0,1219	0.121	0
P22	0,137	0.137	0
P11	0.062	0.062	0
P22	0.0167	0.016	0

Вывод:  Из таблицы видно, что величины отклонений  не превышают 2%, следовательно система смоделирована правильно.

Система с блокировкой

Имеется двухфазная система массового обслуживания, в которой нет возможности разместить очереди перед приборами (рис. 5).

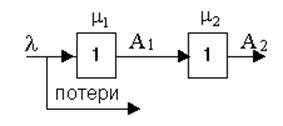
Система дифференциальных уравнений

  

Для стационарного режима работы получаем такую систему алгебраических уравнений:

,                                                                               (1)

,                                                                      (2)

,                                                        (3)